 https://orcid.org/0000-0002-4048-9838
https://orcid.org/0000-0002-4048-9838
POSITIONS
Feel free to spontaneously apply for an internship or a PhD.
Maître de conférences à Sorbonne Université
laura.messio(at)lptmc.jussieu.fr
4 place Jussieu, 75005 Paris
tower 12, 5th floor, corridor 12-13, room 516
Mots clés : systèmes magnétiques frustrés 2D, liquides de spins, solides de liens de valence,
ordre magnétique, ordre par le désordre, vortex, chiralité, algorithme Wang-Landau, systèmes fortement corrélés hors équilibre...
Key words : frustrated 2D spin systems, spin liquids, valence bond solids,
magnetic order, order by disorder, vortices, chirality, Wang-Landau algorithm, out of equilibrium strongly correlated systems...
Bref CV:
- 2023 : HDR
- Depuis 2013 : Maître de Conférence au LPTMC
- 2012-2013 : Post-doctorat dans le groupe d'Olivier Parcollet, à l'IPhT, CEA, Saclay
- 2010-2012 : Post-doctorat dans le groupe de Frédéric Mila, à l'ITP, EPFL, Lausanne, avec enseignement.
- 2007-2010 : Thèse dirigée par Claire Lhuillier et Grégoire Misguish, au LPTMC, avec monitorat.
- 2006-2007 : Master 2 Systèmes Complexes, UPMC
- 2004-2008 : ENS Cachan
Link to arXiv with almost all my publications: link arXiv Messio, except these two:
The influence of surface tension gradients on drop coalescence
F. Blanchette, L. Messio and J. W. M. Bush,
Physics of Fluids, 21, 072107 (2009).
Experimental observation using particle image velocimetry of inertial waves in a rotating fluid [Site du FAST]
L. Messio, C. Morize, M. Rabaud and F. Moisy,
Exp. Fluids 2007, 44, 519-528 (2008).
Mon manuscrit de thèse, ainsi que la présentation se trouvent sur le site des [Thèses en ligne]
(Titre : Etats fondamentaux et excitations de systèmes magnétiques frustrés, du classique au quantique)
I work on spin models encountered in a large number of experimental compounds like Herbertsmithite, Kapellasite, Vesignieite... All these materials are well described by interacting spins S=1/2 on the nodes of a kagome lattice (they are Mott insulators).


I am interested in the description and characterization of all these phases and in the different methods used to track them. Among them are Schwinger boson mean-field theory, exact diagonalization, quantum Monte Carlo simulations, high temperature series expansions...
Spin liquids
Spin liquids are exotic phases quite difficult to apprehend as they are often defined as phases were no symmetry is broken. They are unordered... but not disordered as a high temperature phase: they have fractional excitations, and sometimes topologial properties. Phase transitions between different spin liquids can occur.
Two very different and widely used mean-field theories easily lead to the obtention of spin liquids: the fermionic and bosonic mean-field theories. Both of them are used on spin models and rely on self-consistent conditions on link-parameters, called an Ansatz. Depending on the symmetry imposed to the ground state, the Ansatz has to verify other constraints encoded in the projective symmetry group.
The projective symmetry group classification distinguish the different spin liquids through fluxes. We have adapted this theory to include time-reversal symmetry breaking phases (Phys. Rev. B, 87, 125127 (2013), Phys. Rev. B 93, 094437 (2016)), and applied it to the kagome lattice with first neighbor interactions ( Phys. Rev. B 92, 060407 (2015)) and with Dzyaloshinskii-Moriya interaction (Phys. Rev. Lett., 108, 207204 (2012), Phys. Rev. L 118, 267201 (2017) to describe Herbertsmithite. In the case of Kapellasite, further neighbor interactions are needed (Phys. Rev. Lett., 109, 037208 (2012)).
Néel ordered phases
Frustration (as encountered on the antiferromagnetic triangle), induces unusual Néel orders. From symmetry considerations, a list of 'symmetric' Néel orders can be established, leading to new proposals for the ground states of kagome compounds. For example, the cuboc2 order is supposed to have similarities with the spin liquid encountered in Kapellasite, whereas the cuboc1 order is one of the many degenerate ground state of the kagome antiferromagnet.
cuboc1 order
The classical limit of these frustrated spin models, although their apparent simplicity, is already a very rich problem. The possibility to obtain chiral orders and vortices in long range ordered classical phases has been studied in Phys. Rev. B, 83, 184401 (2011).
Electronic out of equilibrium systems
I am also interested in out of equilibrium strongly correlated systems and participate to the [TRIQS] project.
A new algorithm describing the real time evolution of interacting quantum dots, using the Keldysh technic, has been elaborated in Computer Physics Communications 196, 398 (2015)
High temperature series expansions
The partition function Z of a spin system can be expanded in powers of beta, the inverse temperature (high temperature series expansions). ln(Z)/N is well defined in the thermodynamic limit (N is the number of sites), and can directly be expanded in this limit.
In Phys. Rev. B 101, 140403, a method previously defined as the entropy method is generalized and applied to the antiferromagnetic kagome lattice, with several perturbations (impurities, Ising anisotropy, DM interactions, further neighbor interactions...).
With Laurent Pierre and Bernard Bernu, an efficient algorithm has been written (code publicly available here) for Heisenberg models in the presence of a magnetic field SciPostPhys 17, 105 (2024) .
Phase transitions induced by the order by disorder mechanism
In some situations, the ground state is accidentally degenerate, but entropic effects lift this degeneracy. Thus, a symmetry can be broken at finite temperature due to thermal order by disorder. It was studied in the case of the classical and quantum kagome lattice with first and third neighbor interactions (PhysRevB 102, 214424 (2020)) using spin waves, Monte Carlo simulations and high temperature series expansions. A finite value of the spin (quantum model) leads to quantum order by disorder, that selects the same collinear phase.
The order by disorder phenomena occurs in the octahedral phase (phi is such that 1=cos(phi), J3=sin(phi)).
The J3 exchange defines three square lattices (middle) that orient independently in the ground state of the octahedral phase.
The set of ground states can be represented by an inflated tetrahedra (right). The degeneracy is lifted by thermal or quantum fluctuations, favoring colinear states (red states).
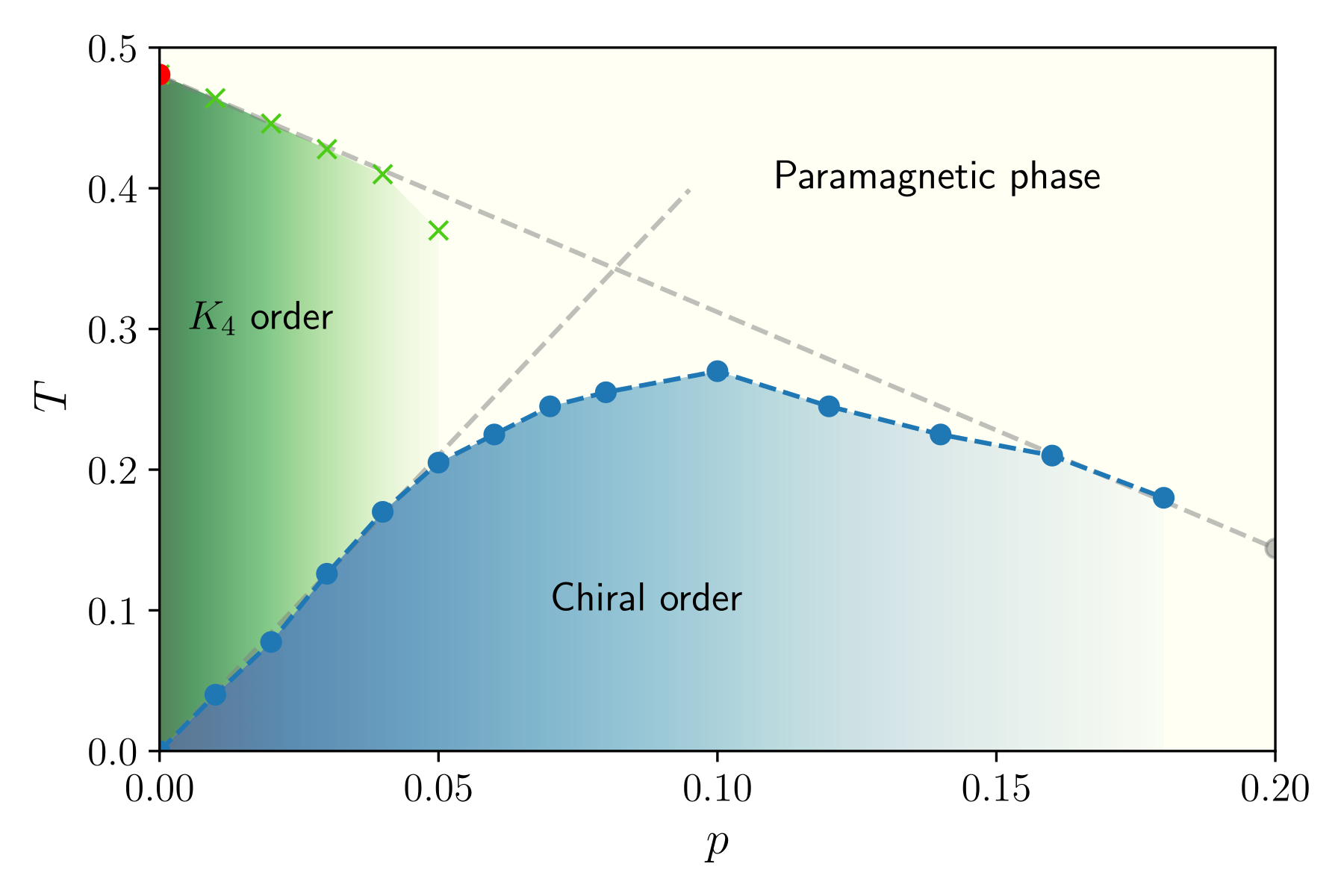
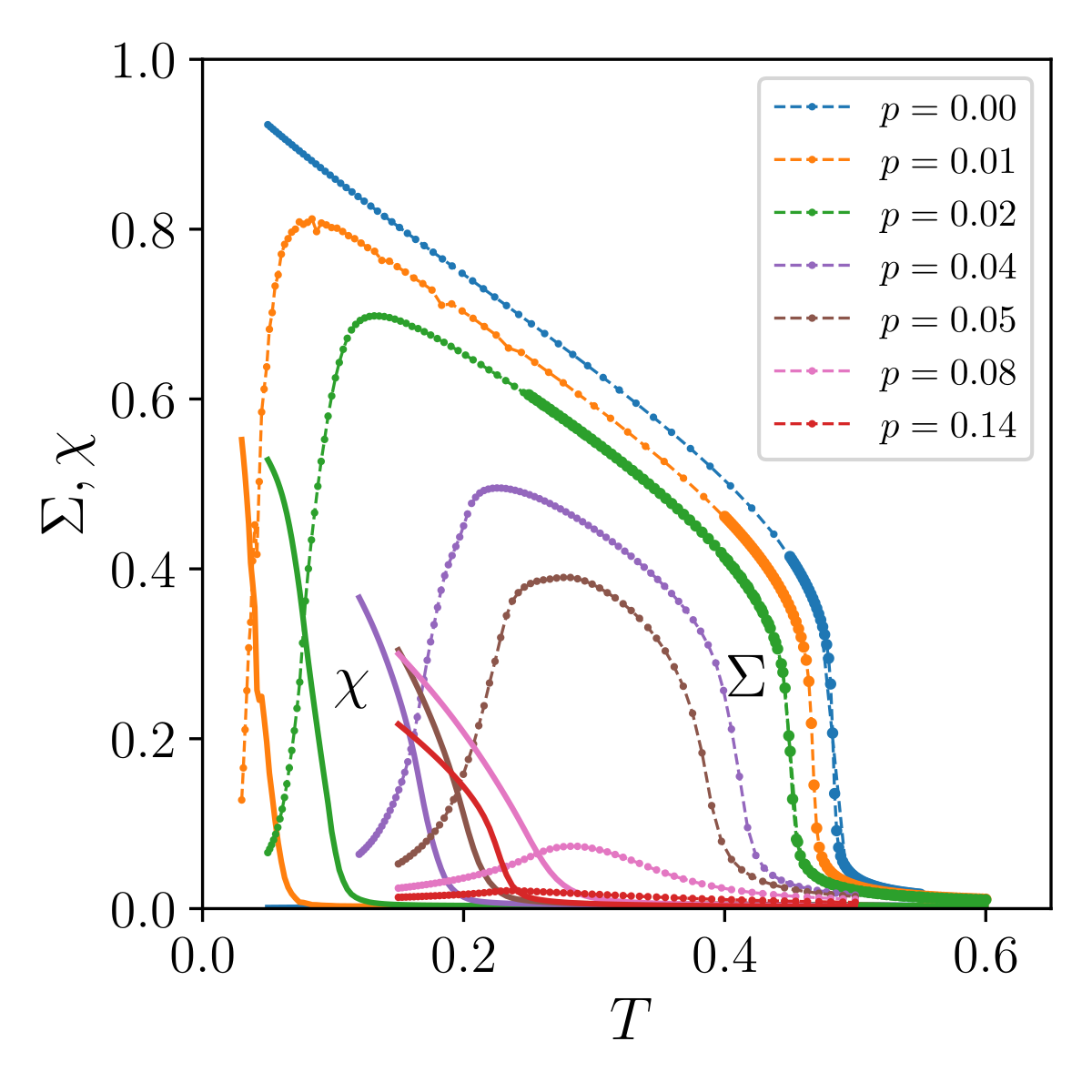
In the presence of a rate p of vacancies in the lattice, another type of order by disorder is in concurrence with thermal or quantum order by disorder : quenched order by disorder. It selects the least-collinear states, and in the previous case on kagome, favors a chiral phase.
TD : Mécanique quantique en L3 à SU (2021-?)
TD : Physique de la matière condensée en M2 de Physique [ICFP] à l'ENS (2016-2021)
TD "The Hubbard model on two sites, the Heisenberg Hamiltonian"
[TD_Hubbard2sites_Heisenberg_enonce]
TD "Graphène"
[TD_Graphene_part1_enonce]
TD "Fonctions de Green"
[TD_Greens_functions_enonce]
TD "Courant stationnaire"
[TD_Stationary_current_enonce]
TD "Règle de somme de Friedel"
[TD_FriedelSumRule_enonce]
TD "Modèle de Gross-Neveu"
[TD_GrossNeveu_enonce]
TD "Thérie de Landau des liquides de Fermi"
[TD_LandauFermiLiquid_enonce]
Version plus détaillée :
[TD_LandauFermiLiquidLastVersion_enonce]
TD et RP : Energie et entropie en L1(PCGI) 1P003 à Sorbonne Université (2017-2019)
TD et TP : Physique numérique en L2 de Physique (Python) [2P022] à l'[UPMC] (2013-2014)
TD et TP : Physique numérique en L3 de Physique (C++) [3P002] à l'[UPMC] (2013-2017)
TD et TP : Physique numérique en L3 de Physique à l'[ENS Cachan], parcours [Phytem] (2013-2018)
TD : Physique statistique I de M1 en Physique a l'[EPFL] (2011-2012)
TD : Mécanique quantique II de M1 a l'[EPFL] (2010-2012)
TD : physique (LP104) en L1 BGPC (Biologie-Géologie-Physique-Chimie) a l'[UPMC] (2008-2010)
Cours et TD : Eléments d'algorithmique en prépa HEC (niveau L1) voie scientifique au lycee Hélene Boucher (2007-2008)
[énoncé TD1] et [corrigé TD1]
[énoncé TD2] et [corrigé TD2]
[énoncé TD3] et [corrigé TD3]
[énoncé TD4] et [corrigé TD4]
[énoncé TD5] et [corrigé TD5]
[énoncé TD6] et [corrigé TD6]
[énoncé TD7] et [corrigé TD7]
avec pour terminer des exercices d'entraînement inspirés de concours : [énoncé TD8]





