Laboratoire de Physique Théorique de la Matière Condensée

Aurélien GRABSCH

CNRS researcher at LPTMC, Sorbonne Université

e-mail: aurelien (dot) grabsch (at) sorbonne-universite.fr

ORCID iD iconorcid.org/0000-0003-4316-5190

CNRS LPTMC SU

  • Current fluctuations in the symmetric exclusion process beyond the one-dimensional geometry
    Théotim Berlioz, Davide Venturelli, Aurélien Grabsch, Olivier Bénichou
    arXiv:2407.14317
  • Semi-infinite simple exclusion process: from current fluctuations to target survival
    Aurélien Grabsch, Hiroki Moriya, Kirone Mallick, Tomohiro Sasamoto, Olivier Bénichou
    arXiv:2404.18481
  • Tracer diffusion beyond Gaussian behavior: explicit results for general single-file systems
    Aurélien Grabsch, Olivier Bénichou
    Phys. Rev. Lett. 132, 217101 (2024)
    arXiv:2401.13409

 

 

 

 

 

 

 

 

 

Keywords: statistical physics, interacting particle systems, stochastic processes, large deviations, condensed matter theory, random matrix theory, topology in condensed matter, Majorana zero modes, disordered systems
Single-file systems I am interested in the physics of single-file systems. These are systems in which particles cannot bypass each other. Following the dynamics of a tracer particle, we observe a subdiffusive behaviour, which originates from strong bath-tracer correlations.
Focusing on paradigmatic models of single-file diffusion, such as the Simple Exclusion Process (SEP), I use analytical tools (master equations, large deviations, ...) to characterise the bath-tracer correlations. In turn, the knowledge of these correlations allow to fully characterise the dynamics of the tracer particle.
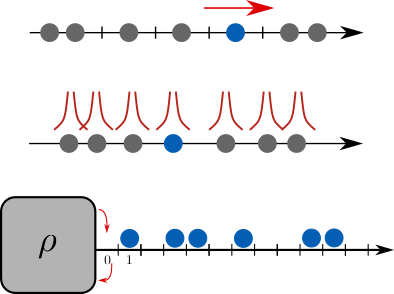Single-file systems From the study of these paradigmatic models, I aim to obtain general laws that apply to more general or realistic models, including driven systems, arbitrary interactions or different geometries.
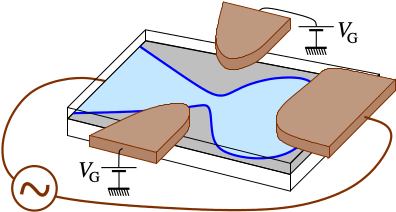RC Quantum Dot I am also interested in the applications of random matrix theory (RMT) to statistical physics, and in particular to quantum transport. For instance, the complex dynamics of chaotic cavities, like quantum dots, can be well described by a statistical approach. This consists in taking a random scattering matrix to characterize transport through the system. Many relevant physical quantities (like conductance, resistance,...) can be expressed in terms of the eigenvalues of the scattering matrix, or related matrices.
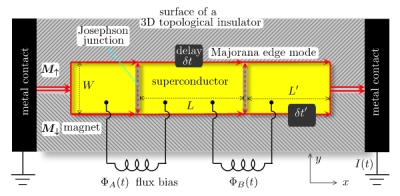Braiding edge vortices During my first postdoc, I worked on topological properties of condensed matter systems. Topological superconductors can support Majorana zero-modes (midgap states bound to a defect). These zero modes have non-Abelian statistics: they are neither bosons nor fermions, and can be used for the realisation of topologically protected quantum computations. Topological superconductors also possess non-Abelian excitations of the chiral edge modes: the edge vortices. Unlike the Majorana zero-modes which are fixed, the edge vortices have the advantage of propagating along the chiral edge modes. I am investigating the possibility to demonstrate the non-Abelian nature of the edge vortices, and their possible use for the realisation of topologically protected quantum computations.
Lyapunov exponents I am also interested in disordered systems. It is well known that wave functions in 1D in a random potential are localized (Anderson localization). The localization length have been computed for diverse models of disorder. However the 2D case is still out of reach.
I mostly focus on models of multichannel disordered wires which describe an intermediate situation, using matrix Langevin equations.

 

 

    • 2020-2022: Postdoc at LPTMC, Sorbonne Université (Paris)

      With Olivier Bénichou

 

Enseignements à Sorbonne Université :

  • TD+TP de Mécanique Physique (L1), 2023-

Enseignements à l'Université Paris-Sud :

  • Cours-TD de physique quantique (L3), 2015-2018
  • TD Programmation et données numériques (M1), 2015-2017