Laboratoire de Physique Théorique de la Matière Condensée

Aurélien GRABSCH

CNRS researcher at LPTMC, Sorbonne Université

e-mail: aurelien (dot) grabsch (at) sorbonne-universite.fr

ORCID iD iconorcid.org/0000-0003-4316-5190

CNRS LPTMC SU

  1. Full stochastic dynamics of a tracer in a dense single-file system
    Alexis Poncet, Aurélien Grabsch, Olivier Bénichou
    arXiv:2505.21446
  2. Exact large-scale correlations in diffusive systems with general interactions: explicit characterisation without the Dean--Kawasaki equation
    Aurélien Grabsch, Davide Venturelli, Olivier Bénichou
    arXiv:2504.08560
  3. Dynamics of soft interacting particles on a comb
    Davide Venturelli, Pierre Illien, Aurélien Grabsch, Olivier Bénichou
    J. Phys. A 58 215001 (2025)
    arXiv:2502.16951
  1. Tracer and current fluctuations in driven diffusive systems
    Théotim Berlioz, Olivier Bénichou, Aurélien Grabsch
    Phys. Rev. Lett. 134, 247101 (2025)
    arXiv:2412.14661
  2. Universal scale-free decay of spatial correlations in d-dimensional interacting particle systems
    Davide Venturelli, Pierre Illien, Aurélien Grabsch, Olivier Bénichou
    arXiv:2411.09326
  3. Current fluctuations in the symmetric exclusion process beyond the one-dimensional geometry
    Théotim Berlioz, Davide Venturelli, Aurélien Grabsch, Olivier Bénichou
    J. Stat. Mech. (2024) 113208
    arXiv:2407.14317
  4. Semi-infinite simple exclusion process: from current fluctuations to target survival
    Aurélien Grabsch, Hiroki Moriya, Kirone Mallick, Tomohiro Sasamoto, Olivier Bénichou
    Phys. Rev. Lett. 133, 117102 (2024)
    arXiv:2404.18481
  5. Tracer diffusion beyond Gaussian behavior: explicit results for general single-file systems
    Aurélien Grabsch, Olivier Bénichou
    Phys. Rev. Lett. 132, 217101 (2024)
    arXiv:2401.13409
  1. Joint distribution of currents in the symmetric exclusion process
    Aurélien Grabsch, Pierre Rizkallah, Olivier Bénichou
    SciPost Phys. 16, 016 (2024)
    arXiv:2307.02374
  2. From Particle Currents to Tracer Diffusion: Universal Correlation Profiles in Single-File Dynamics
    Aurélien Grabsch, Théotim Berlioz, Pierre Rizkallah, Pierre Illien, Olivier Bénichou
    Phys. Rev. Lett. 132, 037102 (2024)
    arXiv:2306.13516
  3. Exact spatial correlations in single-file diffusion
    Aurélien Grabsch, Pierre Rizkallah, Alexis Poncet, Pierre Illien, Olivier Bénichou
    Phys. Rev. E 107, 044131 (2023)
    arXiv:2302.02929
  1. Driven tracer in the Symmetric Exclusion Process: linear response and beyond
    Aurélien Grabsch, Pierre Rizkallah, Pierre Illien, Olivier Bénichou
    Phys. Rev. Lett. 130, 020402 (2023)
    arXiv:2207.13079
  2. Duality relations in single-file diffusion
    Pierre Rizkallah, Aurélien Grabsch, Pierre Illien, Olivier Bénichou
    J. Stat. Mech. (2023) 013202
    arXiv:2207.07549
  3. Exact time dependence of the cumulants of a tracer position in a dense lattice gas
    Alexis Poncet, Aurélien Grabsch, Olivier Bénichou, Pierre Illien
    Phys. Rev. E 105, 054139 (2022)
    arXiv:2202.09278
  1. General truncated linear statistics for the top eigenvalues of random matrices
    Aurélien Grabsch
    J. Phys. A 55 124001 (2022) for the special issue Emerging Talents 2021
    arXiv:2111.09004
  2. Exact closure and solution for spatial correlations in single-file diffusion
    Aurélien Grabsch, Alexis Poncet, Pierre Rizkallah, Pierre Illien, Olivier Bénichou
    Sci. Adv. 8, eabm5043 (2022)
    arXiv:2110.09269
  3. Generalized Correlation Profiles in Single-File Systems
    Alexis Poncet, Aurélien Grabsch, Pierre Illien, Olivier Bénichou
    Phys. Rev. Lett. 127, 220601 (2021)
    arXiv:2103.13083
  1. Half-integer charge injection by a Josephson junction without excess noise
    F. Hassler, A. Grabsch, M.J. Pacholski, D.O. Oriekhov, O. Ovdat, I. Adagideli, C.W.J. Beenakker
    Phys. Rev. B 102, 045431 (2020)
    arXiv:2005.08655
  2. Wigner-Smith matrix, exponential functional of the matrix Brownian motion and matrix Dufresne identity
    A. Grabsch, C. Texier
    J. Phys. A: Math. Theor. 53 425003 (2020)
    arXiv:2002.12077
  1. Localization landscape for Dirac fermions
    G. Lemut, M. J. Pacholski, O. Ovdat, A. Grabsch, J. Tworzydło, C.W.J. Beenakker
    Phys. Rev. B 101, 081405(R) (2020)
    arXiv:1911.04919
  2. Dynamical signatures of ground-state degeneracy to discriminate against Andreev levels in a Majorana fusion experiment
    Aurélien Grabsch, Yevheniia Cheipesh, Carlo W.J. Beenakker
    Adv. Quantum Technol. 2019, 1900110
    arXiv:1909.08335
  3. Distribution of the Wigner-Smith time-delay matrix for chaotic cavities with absorption and coupled Coulomb gases
    Aurélien Grabsch
    J. Phys. A 53(2) 025202 (2019)
    arXiv:1909.01002
  4. Time-resolved electrical detection of chiral edge vortex braiding
    I. Adagideli, F. Hassler, A. Grabsch, M. Pacholski, C.W.J. Beenakker
    SciPost Phys. 8, 013 (2020)
    arXiv:1907.02422
  5. Pfaffian formula for fermion parity fluctuations in a superconductor and application to Majorana fusion detection
    Aurélien Grabsch, Yevheniia Cheipesh, Carlo W.J. Beenakker
    Ann. Phys. (Berlin) 2019, 1900129
    arXiv:1903.11498
  1. Electrical detection of the Majorana fusion rule for chiral edge vortices in a topological superconductor
    Carlo W.J. Beenakker, Aurélien Grabsch, Yaroslav Herasymenko
    SciPost Phys. 6, 022 (2019)
    arXiv:1812.01444
  2. Wigner-Smith time-delay matrix in chaotic cavities with non-ideal contacts
    Aurélien Grabsch, Dmitry V. Savin, Christophe Texier
    J. Phys. A 51(40) 404001 (2018) (Special issue Random Matrices: the first 90 years)
    arXiv:1804.09580
  3. Correlations of occupation numbers in the canonical ensemble and application to BEC in a 1D harmonic trap
    Olivier Giraud, Aurélien Grabsch, Christophe Texier
    Phys. Rev. A 97, 053615 (2018)
    arXiv:1802.02555
  1. Fluctuations of observables for free fermions in a harmonic trap at finite temperature
    Aurélien Grabsch, Satya N. Majumdar, Grégory Schehr, Christophe Texier
    SciPost Phys. 4, 014 (2018)
    arXiv:1711.07770
  2. Extremes of 2d Coulomb gas: universal intermediate deviation regime
    Bertrand Lacroix-A-Chez-Toine, Aurélien Grabsch, Satya N. Majumdar, Grégory Schehr
    J. Stat. Mech. (2018) 013203
    arXiv:1710.06222
  1. Truncated linear statistics associated with the eigenvalues of random matrices II. Partial sums over proper time delays for chaotic quantum dots
    Aurélien Grabsch, Satya N. Majumdar and Christophe Texier
    J. Stat. Phys. 167(2) 1452–1488 (2017)
    arXiv:1612.05469
  2. Truncated linear statistics associated with the top eigenvalues of random matrices.
    Aurélien Grabsch, Satya N. Majumdar and Christophe Texier
    J. Stat. Phys. 167(2), 234-259 (2017)
    arXiv:1609.08296
  3. Distribution of spectral linear statistics on random matrices beyond the large deviation function – Wigner time delay in multichannel disordered wires.
    Aurélien Grabsch and Christophe Texier
    J. Phys. A 49 465002 (2016)
    arXiv:1602.03370
  1. Topological phase transitions in the 1D multichannel Dirac equation with random mass and a random matrix model.
    Aurélien Grabsch and Christophe Texier
    Europhys. Lett. 116, 17004 (2016)
    arXiv:1506.05322
  1. Capacitance and charge relaxation resistance of chaotic cavities - Joint distribution of two linear statistics in the Laguerre ensemble of random matrices.
    Aurélien Grabsch and Christophe Texier
    Europhys. Lett. 109, 50004 (2015)
    arXiv:1407.3302
  1. One-dimensional disordered quantum mechanics and Sinai diffusion with random absorbers.
    Aurélien Grabsch, Christophe Texier and Yves Tourigny
    J. Stat. Phys. 155(2), 237-276 (2014)
    arXiv:1310.6519

Keywords: statistical physics, interacting particle systems, stochastic processes, large deviations, condensed matter theory, random matrix theory, topology in condensed matter, Majorana zero modes, disordered systems
Single-file systems I am interested in the physics of single-file systems. These are systems in which particles cannot bypass each other. Following the dynamics of a tracer particle, we observe a subdiffusive behaviour, which originates from strong bath-tracer correlations.
Focusing on paradigmatic models of single-file diffusion, such as the Simple Exclusion Process (SEP), I use analytical tools (master equations, large deviations, ...) to characterise the bath-tracer correlations. In turn, the knowledge of these correlations allow to fully characterise the dynamics of the tracer particle.
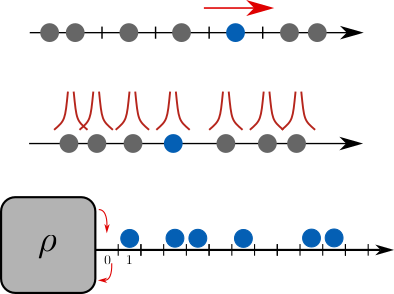Single-file systems From the study of these paradigmatic models, I aim to obtain general laws that apply to more general or realistic models, including driven systems, arbitrary interactions or different geometries.
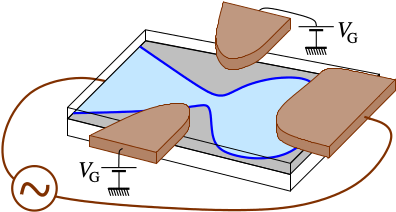RC Quantum Dot I am also interested in the applications of random matrix theory (RMT) to statistical physics, and in particular to quantum transport. For instance, the complex dynamics of chaotic cavities, like quantum dots, can be well described by a statistical approach. This consists in taking a random scattering matrix to characterize transport through the system. Many relevant physical quantities (like conductance, resistance,...) can be expressed in terms of the eigenvalues of the scattering matrix, or related matrices.
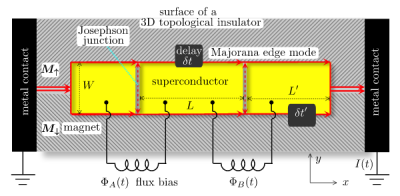Braiding edge vortices During my first postdoc, I worked on topological properties of condensed matter systems. Topological superconductors can support Majorana zero-modes (midgap states bound to a defect). These zero modes have non-Abelian statistics: they are neither bosons nor fermions, and can be used for the realisation of topologically protected quantum computations. Topological superconductors also possess non-Abelian excitations of the chiral edge modes: the edge vortices. Unlike the Majorana zero-modes which are fixed, the edge vortices have the advantage of propagating along the chiral edge modes. I am investigating the possibility to demonstrate the non-Abelian nature of the edge vortices, and their possible use for the realisation of topologically protected quantum computations.
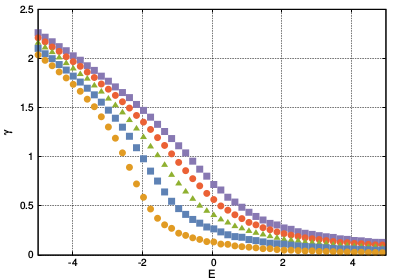Lyapunov exponents I am also interested in disordered systems. It is well known that wave functions in 1D in a random potential are localized (Anderson localization). The localization length have been computed for diverse models of disorder. However the 2D case is still out of reach.
I mostly focus on models of multichannel disordered wires which describe an intermediate situation, using matrix Langevin equations.
  • Since 2022: CNRS researcher (chargé de recherche) at LPTMC
  • 2020-2022: Postdoc at LPTMC, Sorbonne Université (Paris)
    With Olivier Bénichou

Enseignements à Sorbonne Université :

  • TD+TP de Mécanique Physique (L1), 2023-

Enseignements à l'Université Paris-Sud :

  • Cours-TD de physique quantique (L3), 2015-2018
  • TD Programmation et données numériques (M1), 2015-2017