TD 5 Cinétique chimique.

I. Equation différentielle linéaire à coefficients constants.

Réaction du premier ordre

On considère la réaction chimique suivante :
Ecrire l'équation différentielle de la cinétique pour la concentration x de l'espèce X. En utilisant l'instruction dsolve déterminer la solution générale en fonction de k1.
On suppose que x(0)=1 et k1=1/5. Déterminer la solution dans ce cas (On utilisera les options de dsolve pour ajouter une condition initiale et l'instruction subs pour donner une valeur numérique à k1). Tracer la solution sur un graphe pour t compris entre 0 et 15.

> eq1:=diff(x(t),t)+k1*x(t);

> dsolve(eq1,x(t));

> res1:=dsolve({subs(k1=1/5,eq1),x(0)=1},x(t));

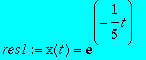
> plot(rhs(res1),t=0..15);

Réaction équilibrée

On considère la réaction chimique equilibrée suivante :

Ecrire les équations différentielles de la cinétique pour les concentration x et y des espèces X. et Y. En utilisant l'instruction dsolve déterminer la solution générale en fonction de k1 et de k2.
On ajoute la condition initiale x(0)+y(0)=1. En supposant que k1 et k2 sont positifs (on utilisera l'instruction assume ), montrer que les concentrations de X et Y tendent vers des valeurs indépendantes des conditions initiales que l'on déterminera (On utilisera l'instruction limit ).
On suppose que k1=0.1 et k2=0.4. Les conditions initiales sont x(0)=1 et y(0)=0. Tracer sur un même graphe x(t) et y(t) pour t compris entre 0 et 10.

> eq2:=diff(x(t),t)=-k1*x(t)+k2*y(t);

> eq3:=diff(y(t),t)=k1*x(t)-k2*y(t);

> res2:=dsolve({eq2,eq3,x(0)+y(0)=1},{x(t),y(t)});

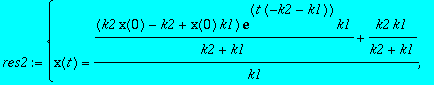
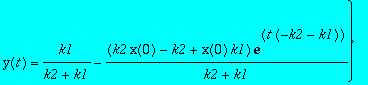
> yinf:=limit(rhs(res2[1]),assume(k1>0,k2>0),t=infinity);

> xinf:=limit(rhs(res2[2]),assume(k1>0,k2>0),t=infinity);

> res4:=dsolve({subs(k1=1/10,k2=4/10,eq2),subs(k1=1/10,k2=4/10,eq3),x(0)=1,y(0)=0},{x(t),y(t)});

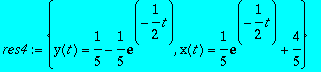
> plot({rhs(res4[1]),rhs(res4[2])},t=0..10);

II. Equation différentielle non-linéaire

On considère l'écosystème suivant : la population est constituée de proies (notées X), de prédateurs (notés Y), de nourriture (notée A). Le taux de reproduction des proies est fixé par la quantité de nourriture, le taux de reproduction des prédateurs est fixé par le nombre de proies, et les prédateurs meurent naturellement avec un taux fixé. Ce système est réprésenté par les équations suivantes

B répresente un prédateur mort. Ecrire les équations différentielles pour l'évolution des espéces X et Y (on suppose que la nourriture est constante et égale à a). En utilisant l'instruction DEplot on tracera les solutions de ces équations en prenant k1=k2=a=1 avec k3=1, 0.5, 0.3 (Lire attentivement cette page d'aide). On prendra deux conditions initiales x(0)=0.2 et y(0)=1.2 et ausi x(0)=1 et y(0)=0.7.

> eqc1:=diff(x(t),t)=x(t)*(1-y(t)),diff(y(t),t)=y(t)*(x(t)-1);

> eqc2:=diff(x(t),t)=x(t)*(1-y(t)),diff(y(t),t)=0.5*y(t)*(x(t)-1);

> eqc3:=diff(x(t),t)=x(t)*(1-y(t)),diff(y(t),t)=0.3*y(t)*(x(t)-1);

> with(DEtools):

> DEplot({eqc1},[x(t),y(t)],t=0..30,[[x(0)=0.2,y(0)=1.2],[x(0)=1,y(0)=.7]],stepsize=.2,method=rkf45);

> DEplot({eqc2},[x(t),y(t)],t=0..30,[[x(0)=0.2,y(0)=1.2],[x(0)=1,y(0)=.7]],stepsize=.2,method=rkf45);

> DEplot({eqc3},[x(t),y(t)],t=0..30,[[x(0)=0.2,y(0)=1.2],[x(0)=1,y(0)=.7]],stepsize=.2,method=rkf45);