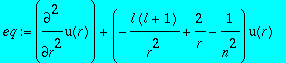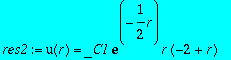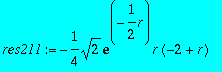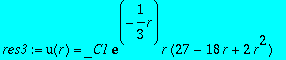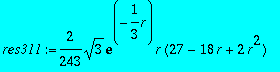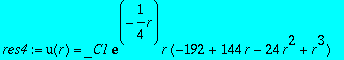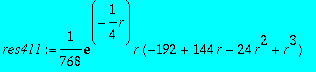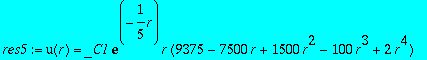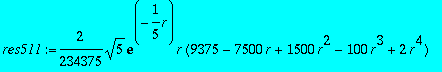Atome d'hydrogène
En mécanique classique, l'équation du mouvement d'un électron soumis au champ électrique d'un proton supposé immobile s'écrit
![E = p^2/(2*m)-e^2/(4*pi*epsilon[0]*r)](images/td518.gif) où p=mv est la quantité de mouvement
où p=mv est la quantité de mouvement
Cette énergie E est une constante du mouvement. Si E est négative, les trajectoires décrites par l'électron sont des ellipses.
En mécanique quantique, un électron soumis au champ électrique du proton est décrit par l'équation de Schrödinger suivante
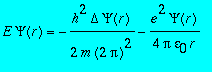 où
où
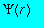 est appelée la fonction d'onde.
est appelée la fonction d'onde.
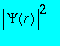 est la probabilité de présence de l'électron au point r . La normalisation de la probabilité impose que
est la probabilité de présence de l'électron au point r . La normalisation de la probabilité impose que
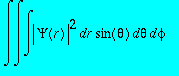 On recherche une solution en coordonnées sphériques de la forme
On recherche une solution en coordonnées sphériques de la forme
*Y[lm](theta,phi)/r](images/td523.gif) où
où
](images/td524.gif) sont les harmoniques sphériques, l un entier positif ou nul, et m un entier compris entre -l et +l.
sont les harmoniques sphériques, l un entier positif ou nul, et m un entier compris entre -l et +l.
On pose :
![E[i] = -m*e^4/(2*(2*epsilon[0]*h)^2)](images/td525.gif) et
et
![a[0] = h^2*epsilon[0]/(pi*m*e^2)](images/td526.gif) . En effectuant le changement de variables suivant E1=E/Ei et r=r/a0, on obtient une équation pour la fonction d'onde
. En effectuant le changement de variables suivant E1=E/Ei et r=r/a0, on obtient une équation pour la fonction d'onde
,`$`(rho,2))+(-l*(l+1)/(rho^2)+2/rho...](images/td527.gif)
On s'intéresse aux solutions pour l=0 (orbitales s). Vérifier que si l'on prend E1=1/n^2 où n est un nombre entier strictement positif, on peut obtenir une solution explicite. Déterminer pour n=1 et n=2, la constante _C1 pour que la probabilité soit normée à l'unité.
Tracer les fonctions pour les valeurs de n allant de 1 à 5 et pour les valeurs de l permises correspondantes.
>
eq:=diff(u(r),r$2)+(-l*(l+1)/r^2+2/r-1/n^2)*u(r);
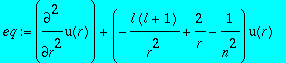
>
res1:=subs(_C2=0,dsolve({subs(n=1,l=0,eq)},u(r)));
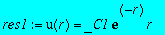
>
res11:=solve(int(rhs(res1)^2,r=0..infinity)=1);
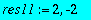
>
res111:=subs(_C1=res11[1],rhs(res1));
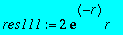
>
res2:=subs(_C2=0,dsolve({subs(n=2,l=0,eq)},u(r)));
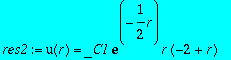
>
res21:=solve(int(rhs(res2)^2,r=0..infinity)=1);
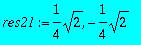
>
res211:=subs(_C1=res21[2],rhs(res2));
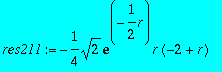
>
res3:=subs(_C2=0,dsolve({subs(n=3,l=0,eq)},u(r)));
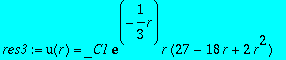
>
res31:=solve(int(rhs(res3)^2,r=0..infinity)=1);
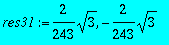
>
res311:=subs(_C1=res31[1],rhs(res3));
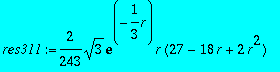
>
res4:=subs(_C2=0,dsolve({subs(n=4,l=0,eq)},u(r)));
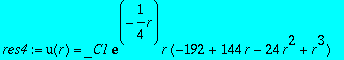
>
res41:=solve(int(rhs(res4)^2,r=0..infinity)=1);
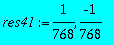
>
res411:=subs(_C1=res41[1],rhs(res4));
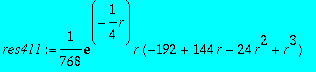
>
res5:=subs(_C2=0,dsolve({subs(n=5,l=0,eq)},u(r)));
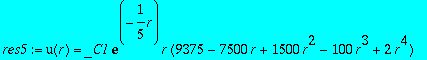
>
res51:=solve(int(rhs(res5)^2,r=0..infinity)=1);
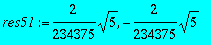
>
res511:=subs(_C1=res51[1],rhs(res5));
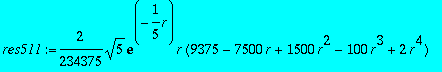
>
plot({seq((res||i||11)^2,i=1..5)},r=0..50);
![E = p^2/(2*m)-e^2/(4*pi*epsilon[0]*r)](images/td518.gif) où p=mv est la quantité de mouvement
où p=mv est la quantité de mouvement 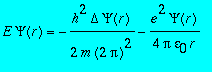 où
où
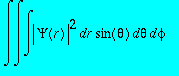 On recherche une solution en coordonnées sphériques de la forme
On recherche une solution en coordonnées sphériques de la forme*Y[lm](theta,phi)/r](images/td523.gif) où
où
![E[i] = -m*e^4/(2*(2*epsilon[0]*h)^2)](images/td525.gif) et
et
![a[0] = h^2*epsilon[0]/(pi*m*e^2)](images/td526.gif) . En effectuant le changement de variables suivant E1=E/Ei et r=r/a0, on obtient une équation pour la fonction d'onde
. En effectuant le changement de variables suivant E1=E/Ei et r=r/a0, on obtient une équation pour la fonction d'onde,`$`(rho,2))+(-l*(l+1)/(rho^2)+2/rho...](images/td527.gif)