Permanent researchers:
M. Barbi, O. Bénichou, M. Dolgushev, A. Grabsch, A. Lesne, M. Micoulaut, J. Mozziconacci, A. Perera, N. Sator, A. Solon, J.-M. Victor, R. Voituriez
Thème 1 : Magmatic liquids modelization (N. Sator)
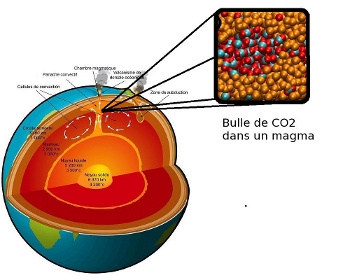
The mantle of the Earth is composed of silicate rocks subjected to extreme conditions. The thermal gradient between the base of the mantle and the crust creates convective motions (solid convection) at the origin of plate tectonics and whose the most spectacular manifestation is volcanism. Indeed, the pressure decreasing as a result of upwelling, mantle partial melting may occur at depth producing silicate melts. Volatiles (H2O, CO2, SO2, noble gases,..) dissolved in these magmas are transported from the mantle to the surface and thus participate in the biogeochemical cycles (e.g. the carbon cycle). To better understand the geodynamics of our planet and its evolution, it is necessary to know the physico-chemical properties of magmatic liquids at the thermodynamic conditions of the mantle (1400-3000K and 0-1350 kbar). It is for this reason that we develop a numerical approach based on molecular dynamics calculations to describe the properties of natural magmas at mantle conditions. We are currently investigating the solubility of carbon, water and noble gases in magmatic liquids of various chemical composition as also as the properties of carbonated liquids produced by melting of carbonate-silicate rock assemblages. These studies are carried out in collaboration with geochemists.
Theme 2: Aqueous mixtures: from solutions to micro-emulsions, a study with tools from the theory of liquids (A. Perera).
Aqueous mixture are the siege of both concentration fluctuations and micro-segregation,the latter which originates from the tendency of water to form nanometer size domains because of the hydrogen bond interaction. These solutions undergo morphological changes when the concentration of either constituents is varied, and appear as molecular emulsions, in analogy with micro-emulsions, from which they differ by 3 orders of magnitudes in scale. This analogy indicate that these systems are in the analog of a Lifshitz state, where fluctuations and particle-emergence compete, with the unvaluable advantage that it can entirely be studied by classical theory of liquids.
Theme 3 : Statistical physics of active matter (A. Solon)
Active matter is made up of particles that dissipate energy to move and exert forces. It includes diverse systems ranging from enzymes and flocks of birds to bacteria and cells. We study the phases and phase transitions of these systems, for example the transition to collective motion or the phase separation induced by motility, using the tools of non-equilibrium statistical physics (minimal models, field theories, numerical simulations).
Theme 4 : Stochastic dynamics of reactive systems and living (O. Bénichou, A. Grabsch, R. Voituriez)
The study of the properties of random walks and their application to the description of various non-equilibrium systems inspired by the physico- chemistry of life is central to the research team . These combine modeling of physical phenomena and the study by analytical methods of general properties of random walks , individual or collective . These contributions are organized primarily along two axes . 1.Marches random and reactivity : A chemical reaction requires firstly meet reactants which must then overcome an energy barrier to yield the products of the reaction . We focus on limited by the first of these steps reactions , ie transportation. In the example of the capture reaction A + B- > B , we have in recent years made explicit answers to the following questions: (i ) the influence of the diffusion coefficients of the reactants on the kinetics of the reaction , (ii ) the influence a catalyst , (iii ) a geometric confinement effect . The latter study revealed a universal dependence of the average first passage time depending on the volume of the system and depending on the distance between the points of departure and arrival . These predictions have been applied to various iconic models of statistical physics ( fractals, disordered media , anomalous diffusion ... ) . Beyond these theoretical aspects , these results led us to introduce the notion of " controlled by the geometry reactions " , where the initial position is a key parameter of the kinetics. 2 . Random walks and research process targets : How long does it take for a " researcher " to find a "target" of unknown position ? This question arises in many contexts , not only in everyday life , typically in the trivial situation where one has lost his keys , but also for foraging by animals. We recently introduced a new type of search strategies, classified as intermittent , combining meticulous research phases and phases of fast moving "blind" , in which the researcher does not attempt to detect the target. We have shown that it is possible to play on time spent in each of these two phases in order to optimize the search time. This model has to account for experimental data to microscopic scales (search for a target sequence of a protein on DNA, reactions in the cell medium ) as well as macroscopic (search for prey by animals ) .
Theme 5 : Multiscale modelization of living matter (M. Barbi, J. Mozziconacci, A. Lesne, J.-M. Victor)
The scientific activity of this team is focused on the physical modelling of living systems, spanning from molecular mechanisms at work in cells to systems biology. The main specificity of our approach is to integrate different time and length scales in our models. This can only be achieved thanks to a genuine combination of different techniques, such as physical simulations, statistical mechanics and network analysis. At the molecular scale, our main interest is the physics of protein/DNA recognition and the specific role played by ions and the DNA sequence. At the nano-scale, our work focuses on the three-dimensional organization of eukaryotic genomes, from the first level of DNA compaction - nucleosomes - to the 30-nm chromatin fiber to the whole cell nucleus. This activity involves many intermingled layers, from the development of in silico single molecule manipulations to the integrative analysis of high throughput biological data. One of the long term goal of these activities is to understand how gene transcription is regulated in cells, a major stake in unveiling the role of genes in normal and pathological functioning of living organisms.
Theme 6 : Rigidity, flexibility and functionality of disordered materials (M. Micoulaut)
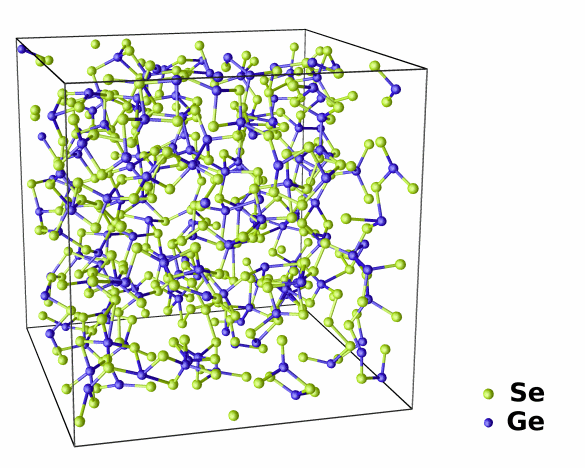This activity at the interface between statistical mechanics , phase transitions , molecular simulations and materials science is based on the theory of rigidity, elegant molecular approach that draws particularly from the concept of mechanical stress used by Maxwell in the nineteenth century to understand the stability of bridges and mechanical mesh. These concepts, extended to disordered covalent networks can be used to quantitatively understand how the effects of chemical composition or pressure change atomic connectivity , topology and state of rigidity amorphous , liquid or glass . Several topics are discussed in this context : 1) Transitions stiffness and intermediate phase : increasing connectivity of an amorphous network giving rise to a transition from flexible - rigid phase is done it randomly or self-organized ? This question opens the theoretical characterization ( phenomenological models or simulations at the molecular level ) isostatic intermediate phase with remarkable properties such as the trend of compactification or low aging vitreous phase. It can even be generalized to the case where the state of rigidity / flexibility is controlled by the pressure or temperature which opens on the relationship between stiffness and glass transition polyamorphism . 2 ) State of rigidity and functionality of materials: The nature of the molecular network ( flexible, rigid ) can be used to devise new features in innovative materials . We have thus demonstrated that flexibility at the atomic scale could promote ionic conduction which helped define a new class of solid electrolytes . Similarly we have undertaken molecular simulation to link the state of rigidity and structural properties of chalcogenide materials " phase change" used in the DVD industry.
Thème 7 : Statistical inference and biological networks (J. Mozziconacci, A. Lesne)
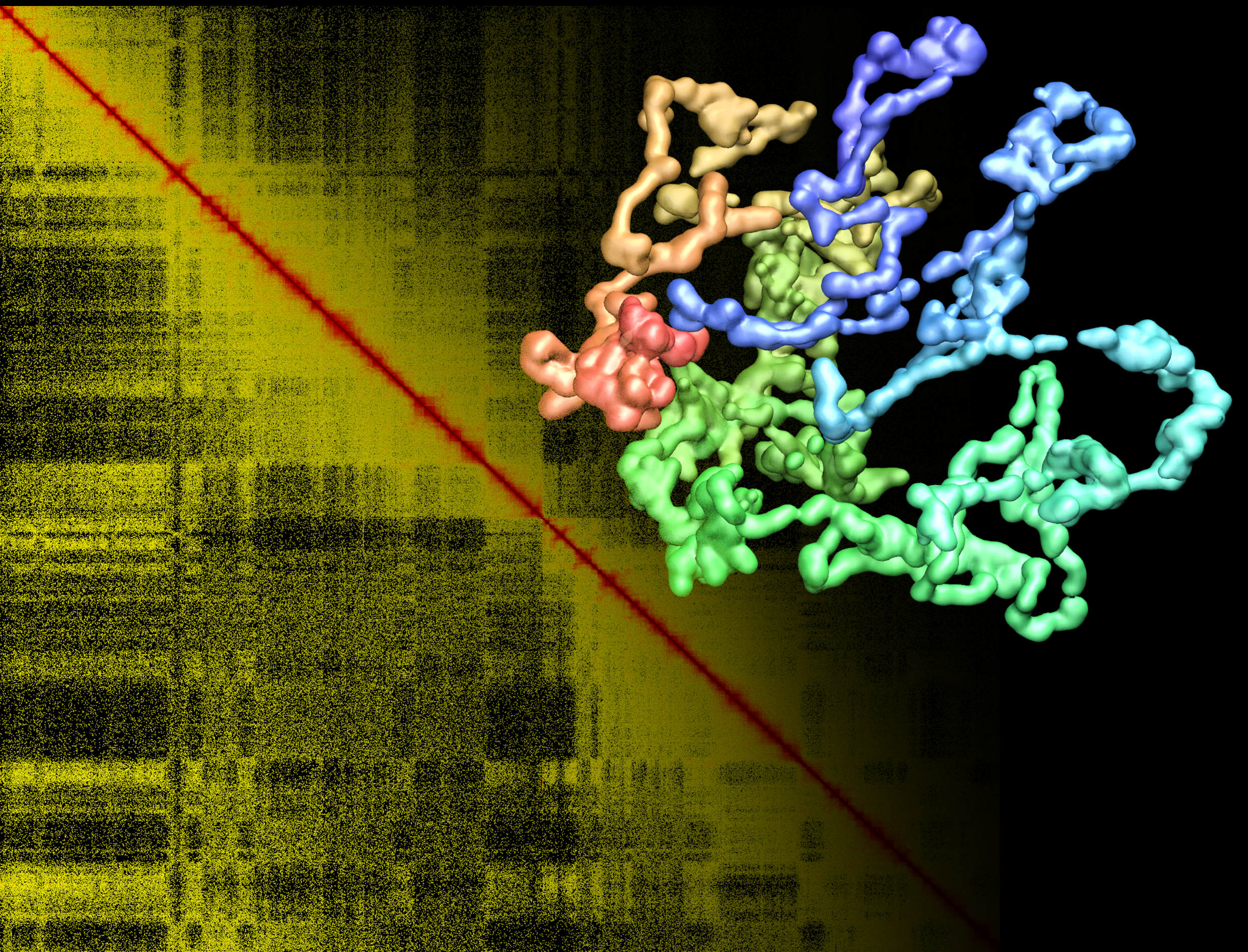
With the development of high-throughput techniques, biology is now faced to an avalanche of data of various types, for instance images of molecular structures, DNA sequences or genomic profiles. To represent in a meaningful way and confront these data to explicatives models, methods from statistical physics and network science are essential. The goal of this research theme is to develop novel quantitative tools and exploit them to better understand the functioning of living systems, with a focus on genome functions.