![V1 := _rtable[138164676]](images/td91.gif)
TD 9 Matrices et Vecteurs
Maple dispose de nombreuses fonctions pour manipuler des matrices et obtenir un grand nombre de résultats. Pour les versions antérieures à la version VI,, ces fonctions étaient regroupées dans la bibliothèque linalg . Dans la version VI, une nouvelle bibliothèque a été mise en place, elle s'appelle LinearAlgebra . Pour charger cette bibliothèque, on tapera l'instruction with( LinearAlgebra ): La syntaxe est très différente avec l'ancienne bibliothèque linalg Nous travaillerons au début avec la nouvelle, et aussi avec l'ancienne par la suite..
Définitions et opérations simples
Il y a au moins deux méthodes pour construire un vecteur (colonne).
V1:=Vector(x,y,z);
V2:=<x,y,z>;
Pour un vecteur (ligne);
V3:=Vector[row]([x,y,z]);
V4:=<x|y|z>;
Tester ces différentes définitions.
> with(LinearAlgebra):
> V1:=Vector([x,y,z]);
![V1 := _rtable[138164676]](images/td91.gif)
> V2:=<x,y,z>;
![V2 := _rtable[138103128]](images/td92.gif)
> V3:=Vector[row]([x,y,z]);
![]()
> V4:=<x|y|z>;
![]()
Il y a plusieurs méthodes pour définir une matrice, à partir de l'instruction Matrix.
1) Méthode ligne à ligne, à partir de listes.
AA:=Matrix([[1,2,3],[4,5,6],[7,8,9]]);
2) Méthode colonne par colonne à partir de vecteur
BB:=Matrix([<1,2,3>,<4,5,6>,<7,8,9>]);
Il existe surtout des raccourcis très utiles
Pour construire en ligne
AA2:=<<1|2|3>,<4|5|6>,<7|8|9>>;
BB2:=<<1,2,3>|<4,5,6>|<7,8,9>>;
Tester à nouveau ces différentes méthodes.
Pour avoir l'élément de la deuxième ligne et troisième colonne
AA[2,3];
> AA:=Matrix([[1,2,3],[4,5,6],[7,8,9]]);
![AA := _rtable[135933496]](images/td95.gif)
> BB:=Matrix([<1,2,3>,<4,5,6>,<7,8,9>]);
![BB := _rtable[136311000]](images/td96.gif)
> AA2:=<<1|2|3>,<4|5|6>,<7|8|9>>;
![AA2 := _rtable[138273104]](images/td97.gif)
> BB2:=<<1,2,3>|<4,5,6>|<7,8,9>>;
![BB2 := _rtable[145512952]](images/td98.gif)
> AA[2,3];
![]()
Initialisation des matrices
Que font les instructions
Matrix(3);
Matrix(3,2);
Matrix(1..3,1..3,5);
Soit la fonctions de deux variables
ff:=(m,n)->cos(m*x)*cos(n*x);
Que donne Matrix(5,ff);
Pour définir une matrice identité
Matrix(3,3,shape=identity);
Pour définir une matrice diagonal
Matrix(3,3,4,shape=diagonal);
> Matrix(3);
![_rtable[146023496]](images/td910.gif)
> Matrix(3,2);
![_rtable[146707732]](images/td911.gif)
> Matrix(1..3,1..3,5);
![_rtable[134626088]](images/td912.gif)
> ff:=(m,n)->cos(m*x)*cos(n*x);
![]()
> FF:=Matrix(5,ff);
![FF := _rtable[134572816]](images/td914.gif)
> Matrix(3,3,shape=identity);
![_rtable[134738588]](images/td915.gif)
> Matrix(3,3,4,shape=diagonal);
![_rtable[134882124]](images/td916.gif)
Opérations
Addition de deux matrices (de même dimension)
Exécuter
AA+BB;
Multiplication de deux matrices
AA2.BB2;
BB2.AA2;
Inverse de matrice
Calculer <<1,2>|<3,0>>^(-1);
Augmentation de lignes
AA3:=<V3,AA>;
Augmentation de colonnes
BB3:=<BB|V1>;
A partir de la matrice BB2, construire une matrice 4x4 dont la ligne superieure est consituée de zeros ainsi que la dernière colonne, et dont la sous-matrice 3x3 en bas à gauche est donnée par BB2;
> AA+BB;
![_rtable[135793940]](images/td917.gif)
> AA2.BB2;
![_rtable[137938712]](images/td918.gif)
> BB2.AA2;
![_rtable[145349384]](images/td919.gif)
> <<1,2>|<3,0>>^(-1);
![_rtable[134771144]](images/td920.gif)
> AA3:=<V3,AA>;
![AA3 := _rtable[135154316]](images/td921.gif)
> <BB|V1>;
![_rtable[135853272]](images/td922.gif)
> V4:=Vector(3);
![V4 := _rtable[135821360]](images/td923.gif)
> BB3:=<BB2|V4>;
![BB3 := _rtable[136942876]](images/td924.gif)
> V5:=Vector[row](4);
![]()
> BB4:=<V5,BB3>;
![BB4 := _rtable[137961188]](images/td926.gif)
Applications: exponentielle de matrices, matrices nilpotentes
Si A est une matrice, alors on définit l'exponentielle de A à partir de la relation
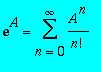 . L'instruction
exponential
permet de calculer directement l'exponentielle de A en utilisant la bibliothèque
linalg
. Calculer aussi la somme pour n=1 à 10 puis n=1 à 20, (on utilisera
evalm
pour calculer explicitement la somme) et vérifier en utilisant l'instruction
evalf
que cette somme converge vers l'exponentielle de A.
. L'instruction
exponential
permet de calculer directement l'exponentielle de A en utilisant la bibliothèque
linalg
. Calculer aussi la somme pour n=1 à 10 puis n=1 à 20, (on utilisera
evalm
pour calculer explicitement la somme) et vérifier en utilisant l'instruction
evalf
que cette somme converge vers l'exponentielle de A.
Calculer l'exponentielle de la matrice
![A := _rtable[7976000]](images/td928.gif)
> A:=<<1,-3>|<1,-2>>;
![A := _rtable[145377876]](images/td929.gif)
> with(linalg):
Warning, the name adjoint has been redefined
Warning, the previous binding of the name GramSchmidt has been removed and it now has an assigned value
Warning, the protected names norm and trace have been redefined and unprotected
> EA:=exponential(A);
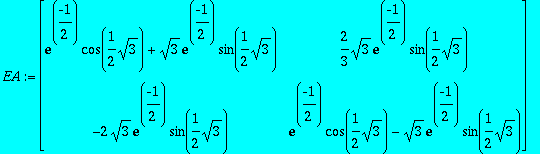
> evalf(evalm(EA));
![matrix([[1.193207349, .5335071953], [-1.600521586, ...](images/td931.gif)
> A10:=evalf(evalm(sum(A^n/n!,n=0..10)));
![A10 := matrix([[1.193207396, .5335072200], [-1.6005...](images/td932.gif)
> A20:=evalf(evalm(sum(A^n/n!,n=0..20)));
![A20 := matrix([[1.193207349, .5335071951], [-1.6005...](images/td933.gif)
Soit une matrice nxn, on appelle une matrice nilpotente une matrice telle que
![]() pour . Déterminer toutes les matrices pour n=2.
pour . Déterminer toutes les matrices pour n=2.
Montrer en utilisant l'instruction Jordanform que toutes les solutions sont équivalentes à des matrices triangulaires supérieures avec une ligne située au dessus de la diagonale composée de 1. Même exercices pour n=3. Afficher toutes les solutions et vérifier a postériori que la propriété de nilpotence est vérifiée.
> A:=<<a,b>|<c,d>>;
![A := _rtable[148046868]](images/td935.gif)
> CC:=A.A;
![CC := _rtable[148211704]](images/td936.gif)
> sols:=solve({seq(seq(CC[i,j],i=1..2),j=1..2)},{a,b,c,d});
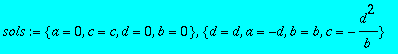
> res1:=subs(sols[1],A);
![res1 := _rtable[134894536]](images/td938.gif)
> res2:=subs(sols[2],A);
![res2 := _rtable[134986792]](images/td939.gif)
> JordanForm(res1);JordanForm(res2);
![_rtable[135639912]](images/td940.gif)
![_rtable[136049116]](images/td941.gif)
> A:=<<a,b,c>|<d,e,f>|<g,h,k>>;
![A := _rtable[137229608]](images/td942.gif)
> CC:=A.A.A;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
> sol2:=solve({seq(seq(CC[i,j],i=1..3),j=1..3)},{a,b,c,d,e,f,g,h,k});
![]()
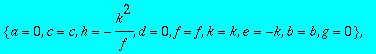
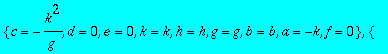
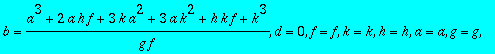
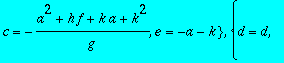
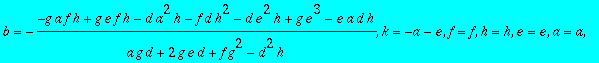
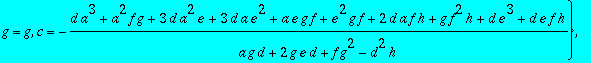
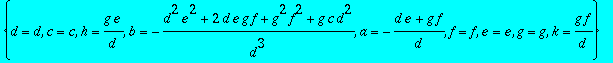
> for i from 1 to 6 do HH||i:=subs(sol2[i],A);od;
![HH1 := _rtable[144872020]](images/td961.gif)
![HH2 := _rtable[145107136]](images/td962.gif)
![HH3 := _rtable[145274788]](images/td963.gif)
![HH4 := _rtable[145219196]](images/td964.gif)
![]()
![]()
![HH5 := _rtable[145419396]](images/td967.gif)
![HH5 := _rtable[145419396]](images/td968.gif)
![HH6 := _rtable[145486888]](images/td969.gif)
> for i from 1 to 6 do map(simplify,HH||i.HH||i.HH||i);od;
![_rtable[150397700]](images/td970.gif)
![_rtable[135725796]](images/td971.gif)
![_rtable[136318724]](images/td972.gif)
![_rtable[137661772]](images/td973.gif)
![_rtable[135846328]](images/td974.gif)
![_rtable[148228860]](images/td975.gif)
> for i from 1 to 6 do JordanForm(HH||i);od;
![_rtable[146964900]](images/td976.gif)
![_rtable[135560084]](images/td977.gif)
![_rtable[136360048]](images/td978.gif)
![_rtable[135729120]](images/td979.gif)
![_rtable[144891080]](images/td980.gif)
![_rtable[136197100]](images/td981.gif)
>
>