TD 8 Oscillateurs en Physique

Les mouvements vibratoires interviennent dans de nombreux phénomènes en physique. Il est possible de visualiser à l'aide de Maple les propriétés associées aux mouvements des oscillateurs.

>

L'oscillateur harmonique

On considère une masse m assujettie à se déplacer le long d'une droite horizontale et soumise à la force de rappel d'un ressort -kx, où k est la constante de raideur et x la position de la particule sur l'axe Ox. L'équation du mouvement est .

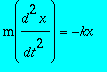et la solution est une fonction sinusoïdale du temps. Ce mouvement peut être représenté dans l'espace des phases, c'est-à-dire dans ce cas, un plan dont les axes sont donnés par la position et la vitesse de la particule.
Dans un tel espace, un mouvement périodique est caractérisé par une trajectoire fermée. En choisissant une unité de temps appropriée, on peut se ramener à une équation où le rapport k/m est égal à 1.

Pour tracer les trajectoires dans l'espace des phases, on charge la bibliothèque with(DEtools):
puis, on utilise l'ordre phaseportrait. Par exemple, l'instruction
phaseportrait ([D(x)(t)=v(t),D(v)(t)=-x(t)],[x(t),v(t)],t=0..10,[[x(0)=0,v(0)=2],[x(0)=0,v(0)=4]],stepsize=.1);
trace dans l'espace des phases deux trajectoires pour un intervalle de temps compris entre 0 et 10, avec les conditions initiales suivantes : x(0)=0, v(0)=2 pour la première trajectoire et v(0)=4 pour la seconde.
Tracer les trajectoires pour une suite de conditions initiales x(0)=0 et v(0)=i pour i allant de -3 à +3. Que remarque-t-on ? Quelle est la propriété physique à l'origine de ce résultat ?

> with(DEtools):

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-x(t)],[x(t),v(t)],t=0..10,[[x(0)=0,v(0)=2],[x(0)=0,v(0)=4]],stepsize=.1);

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-x(t)],[x(t),v(t)],t=0..10,[seq([x(0)=0,v(0)=i],i=-3..3)],stepsize=.1);

On a 3 courbes fermées. Equation invariante par renversement du temps, donc les trajectoires dans l'espace des phases sont identiques pour v0 ou -v0

>

On considère dans un second temps que l'oscillateur est soumis à une force supplémentaire de frottement fluide. L'équation du mouvement est alors
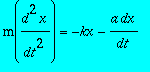.Tracer dans l'espace des phases les trajectoires précédentes pour des valeurs a/m valant 0.1, 1, 2, 4 et pour une suite de conditions initiales x(0)=0 et v(0)=i pour i allant de -2 à +2. . Que note-t-on sur le nombre et la forme de celles-ci ? Pour quelle valeur de a/m observe-t-on un changement de comportement ?

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-0.1*v(t)-x(t)],[x(t),v(t)],t=0..10,[seq([x(0)=0,v(0)=i],i=-2..2)],stepsize=.1);

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-v(t)-x(t)],[x(t),v(t)],t=0..10,[seq([x(0)=0,v(0)=i],i=-2..2)],scene=[x(t),v(t)],stepsize=.1);

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-2*v(t)-x(t)],[x(t),v(t)],t=0..10,[seq([x(0)=0,v(0)=i],i=-2..2)],scene=[x(t),v(t)],stepsize=.1);

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-4*v(t)-x(t)],[x(t),v(t)],t=0..10,[seq([x(0)=0,v(0)=i],i=-2..2)],scene=[x(t),v(t)],stepsize=.1);

Le système esr dissipatif. Le point (0,0) est un attracteur pour l'ensemble des trajectoires. L'invariance par renversement du temps est brisée, les trajectoires avec -v0 et +v0 comme condition initiales ne sont plus superposables. On observe trois régimes psedo-périodique (la trajectoire s'enroule autour du centre), le régime critique (a=2), les trajectoires situées à gauche ou à droite de l'axe y=0 retournent à l'origine sans franchir cet axe. Pour a>2, le régime est apériodique avec des caractéristiques visuelles assez identiques au régime critique.

>

L'oscillateur anharmonique

On considère une masse m assujettie à se déplacer le long d'une droite horizontale et soumise à la force de rappel d'un ressort -kx-gx3, où g est la constante anharmonique. L'équation du mouvement est .

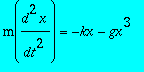Tracer dans l'espace des phases les trajectoires précédentes pour des valeurs g/m valant 0.1 et 1.(On garde k/m=1) Que note-t-on sur le nombre et la forme de celles-ci ?
On considère dans un second temps que l'oscillateur est soumis à une force supplémentaire de frottement fluide de même nature que pour l'oscillateur. Tracer les trajectoires dans l'espace de phase pour les mêmes valeurs de a/m de la partie précédente en prenant g/m =1.

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-x(t)-0.1*x(t)^3],[x(t),v(t)],t=0..20,[seq([x(0)=0,v(0)=i],i=-2..2)],stepsize=.1);

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-x(t)-x(t)^3],[x(t),v(t)],t=0..20,[seq([x(0)=0,v(0)=i],i=-2..2)],stepsize=.1);

Mouvement conservatif. Les trajectoires sont fermées et les trajectoires avec les conditions initiales -v0 et +v0 sont superposables. L'absence d'isochrononisme donnent des trajectoires étirées dont la direction des vitesses. Ces trajectoires redeviennent de plus en plus circulaires pour une energie initiale faible (quasi-isochronisme).

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-x(t)-x(t)^3-0.1*v(t)],[x(t),v(t)],t=0..20,[seq([x(0)=0,v(0)=i],i=-2..2)],stepsize=.1,linecolor=[red,blue,black,yellow,brown]);

> phaseportrait([D(x)(t)=v(t),D(v)(t)=-x(t)-x(t)^3-2*v(t)],[x(t),v(t)],t=0..20,[seq([x(0)=0,v(0)=i],i=-2..2)],linecolor=[red,blue,black,yellow,brown],stepsize=.1);

Les trajectoires convergeant vers l'orgine, l'analyse précédente sur l'oscillateur harmonique amortie est asymptotiquement celle de l'oscillateur anharmonique.

>

Particule dans un double puits de potentiel

On considère une masse m assujettie à se déplacer le long d'une courbe donnée par l'équation z=-x^2/2+x^4/4.

> plot(-x^2/2+x^4/4,x=-2..2);

On peut montrer que le mouvement d'une particule soumise à son poids est donné par l'équation .

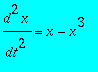Tracer les trajectoires dans l'espace des phases en utilisant des conditions initiales (x(0)=0.5, v(0)=0.2), (x(0)=0.5, v(0)=0.5) et (x(0)=0.5, v(0) =2). Analyser le résultat obtenu. Déterminer la valeur critique de la vitesse pour qu'une particule partant de x=1 effectue un mouvement vibratoire dans l'ensemble des deux puits.

> phaseportrait([D(x)(t)=v(t),D(v)(t)=x(t)-x(t)^3],[x(t),v(t)],t=0..20,[[x(0)=0.5,v(0)=0.2],[x(0)=0.5,v(0)=0.5],[x(0)=0.5,v(0)=2]],linecolor=[red,blue,brown],stepsize=.1);

On voit que si la vitesse initiale est trop faible la trajectoire reste bornée autour d'un minimum. Les oscillations peuvent être fortement anharmoniques

La valeur critique de la vitesse si x(0)=1 correspond à une vitesse où l'énergie mécanique s'annule, soit v=1/sqrt(2).

>

On considère dans un second temps que l'oscillateur est soumis à une force supplémentaire de frottement fluide de même nature que pour l'oscillateur. Tracer les trajectoires dans l'espace de phase pour différentes valeurs du coefficient de frottement fluide.

> phaseportrait([D(x)(t)=v(t),D(v)(t)=x(t)-x(t)^3-0.1*v(t)],[x(t),v(t)],t=0..20,[[x(0)=0.5,v(0)=0.2],[x(0)=0.5,v(0)=0.5],[x(0)=0.5,v(0)=2]],linecolor=[red,blue,brown],stepsize=.1);

> phaseportrait([D(x)(t)=v(t),D(v)(t)=x(t)-x(t)^3-0.5*v(t)],[x(t),v(t)],t=0..20,[[x(0)=0.5,v(0)=0.2],[x(0)=0.5,v(0)=0.5],[x(0)=0.5,v(0)=2]],linecolor=[red,blue,brown],stepsize=.1);

> phaseportrait([D(x)(t)=v(t),D(v)(t)=x(t)-x(t)^3-v(t)],[x(t),v(t)],t=0..20,[[x(0)=0.5,v(0)=0.2],[x(0)=0.5,v(0)=0.5],[x(0)=0.5,v(0)=4]],linecolor=[red,blue,brown],stepsize=.1);

>

>

>