td7.html

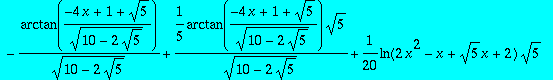
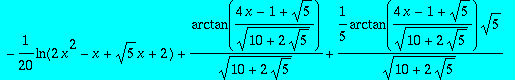
TD 7 Intégration

I. Intégration

I. 1 Primitives

Si les bornes de l'intégration ne sont pas spécifiées, l'instruction int permet de déterminer une primitive d'une fonction.
Exemple :
int(1/(x^5+1),x);

> int(1/(x^5+1),x);

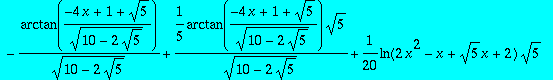
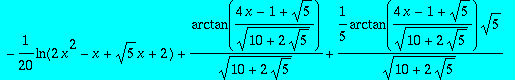
Calculer les primitives de , ,

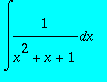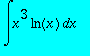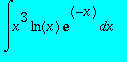
> int(1/(x^2+x+1),x);

> int(x^3*ln(x),x);

> int(x^3*ln(x)*exp(-x),x);

La primitive d'une fonction ne s'exprime pas toujours à partir de fonction simples.
Exemple :
I2:=int(x^2*exp(x^2-x^3),x);
On peut toutefois obtenir un développement limité de l'intégrale précédente en utilisant l'instruction series
series(I2,x,10);
permet de calculer un développement limité de l'intégrale précédente à l'ordre 10.

> I2:=int(x^2*exp(x^2-x^3),x);

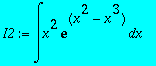
> series(I2,x,10);

I.2 Intégrales définies

Pour des intégrales simples de la forme 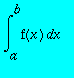, on dispose avec Maple de l'instruction int .
Exemple:

int(4*x^3+2*x^8,x=1..8);

donne le résultat exact de l'intégrale du polynôme entre x=1 et x=8.

> int(4*x^3+2*x^8,x=1..8);

Calculer , , , ,

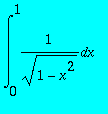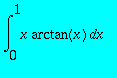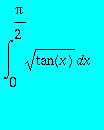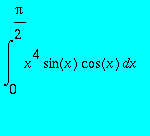> int(1/sqrt(1-x^2),x = 0 .. 1);

> int(x*arctan(x),x = 0 .. 1);

> int(sqrt(tan(x)),x = 0 .. Pi/2);

> int(x^4*sin(x)*cos(x),x = 0 .. Pi/2);

I.3 Intégrales impropres

L'instruction int permet aussi de calculer des intégrales impropres.
Exemple :
int((4*x^3+2*x^8)*exp(-3*x),x=1..infinity);
int(t^4*ln(t)^2/(1+3*t^2)^3,t=0..infinity) ;
Pour connaître une valeur approchée d'une intégrale, on peut utiliser l'instruction evalf . Calculer les intégrales suivantes exactement et/ou de manière approchée.

> int((4*x^3+2*x^8)*exp(-3*x),x=1..infinity);

> int(t^4*ln(t)^2/(1+3*t^2)^3,t=0..infinity) ;

>

Calculer , , ,

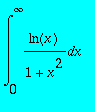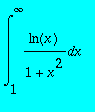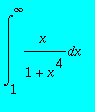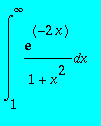
> I32a:=int(ln(x)/(1+x^2),x=0..infinity);

> I32b:=int(ln(x)/(1+x^2),x = 1 .. infinity);evalf(I32b);

> I32c:=int(x/(1+x^4),x = 1 .. infinity);evalf(I32c);

> I32d:=int(exp(-2*x)/(1+x^2),x = 1 .. infinity);evalf(I32c);

I.4. Intégrales avec paramètre

Pour une fonction avec un paramètre, Maple donne parfois une réponse qui peut paraître incomplète.
Exemple :
int(exp(-a*x^2),x=0..infinity);
L'instruction assume permet de faire une hypothèse sur une variable donnée. Dans le cas qui nous intéresse, pour supposer que la partie réelle de a est positive, on introduit l'instruction
assume(a>0) ;
Calculer à nouveau l'intégrale précédente. Noter l'apparition d'un tilde. Rappel : Pour que a puisse être à nouveau une variable quelconque, on réinitialise avec l'instruction a:='a' ;.

Vérifier que l'intégrale précédente redevient indéterminée.

> Ia:=int(exp(-a*x^2),x=0..infinity);

Definite integration: Can't determine if the integral is convergent.

Need to know the sign of --> a

Will now try indefinite integration and then take limits.

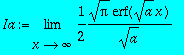
> assume(a>0) ;Ia;

> a:='a';

Calculer 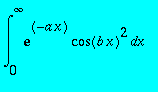avec a>0, 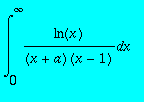, 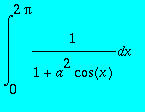avec a compris entre -1 et 1,

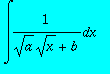
> I3:=int(exp(-a*x)*cos(b*x)^2,x = 0 .. infinity);

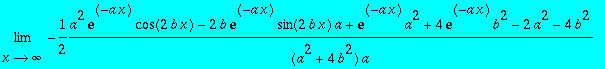
> assume(a>0);I3;

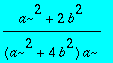
> a:='a';b:='b';

> int(ln(x)/((x+a)*(x-1)),x = 0 .. infinity);

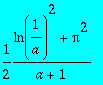
> int(1/(1+a*cos(x)),x = 0 .. 2*Pi);

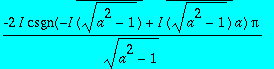
> assume(-1<a, a<1);

> int(1/(1+a*cos(x)),x = 0 .. 2*Pi);

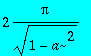
> a:='a';

> int(1/(sqrt(a)*sqrt(x)+b),x);

>

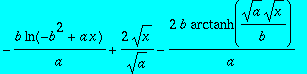
I.5 Intégrales multiples

On peut calculer des intégrales double et triple avec Maple de manière très simple en utilisant l'instruction int de manière successive.

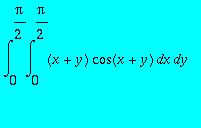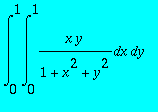
> int(int((x+y)*cos(x+y),x = 0 .. Pi/2),y = 0 .. Pi/2);

> simplify(int(int(x*y/(1+x^2+y^2),x = 0 .. 1),y = 0 .. 1));

II Méthodes d'intégration

Pour calculer une intégrale, il existe un grand nombre de méthodes. Nous allons voir quelques unes de celles-ci. Soit une fonction notée ff.

L'intégrale à calculer est la suivante .

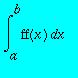La méthode des rectangles estime cette intégrale par la formule :

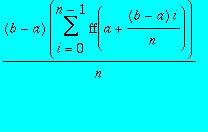Ecrire une procédure rectangle dont les variables sont a, b, n et le nom de la fonction ff.

L'intégrale que nous allons tester est la suivante : .

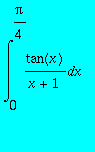Faire le calcul pour n de 50 à 500 avec un pas de 50. (Indication: faire une boucle sur n)

En supposant que la différence entre la valeur exacte et la valeur approchée notée est de la forme , déterminer la valeur de .

La méthode des trapèzes estime cette intégrale par la formule :

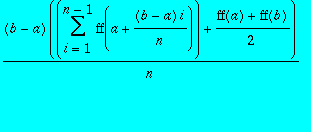Ecrire une procédure trapeze dont les variables sont a, b, n et le nom de la fonction ff.

En supposant que la différence entre la valeur exacte et la valeur approchée notée est la forme , déterminer la valeur de .

Utiliser ensuite l'option Digits:=10; que notez vous?

On veut calculer l'intégrale 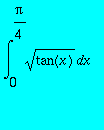. Quelles valeurs de et de trouve-t-on? Conclusion.

> rectangle:=proc(a,b,n::posint,ff)

> local a1,b1,n1,i,delta;

> a1:=a;b1:=b;n1:=n;delta:=(b-a)/n;

> evalf(delta*(sum(ff(a+delta*i),i=0..n-1)));

> end;

> ff:=unapply(tan(x)/(x+1),x);

> valex:=evalf(int(ff(x),x = 0 .. Pi/4));

> for j from 100 to 500 by 50 do
tmp:=abs((valex-rectangle(0,Pi/4,j,ff))/(valex-rectangle(0,Pi/4,(j-50),ff)));
evalf(ln(tmp)/ln(abs((j-50)/j)) );
od;

> trapeze:=proc(a,b,n::posint,ff)

> local a1,b1,n1,i,delta;

> a1:=a;b1:=b;n1:=n;delta:=(b-a)/n;

> evalf(delta*(sum(ff(a+delta*i),i=0..n1-1)+(-ff(a)+ff(b)/2)));

> end;

> Digits:=10;

> for j from 100 to 500 by 50 do
tmp:=abs((valex-trapeze(0,Pi/4,j,ff))/(valex-trapeze(0,Pi/4,(j-50),ff)));
evalf(ln(tmp)/ln(abs((j-50)/j)) );
od;

> gg:=unapply(tan(x)^(1/4),x);

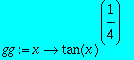
> valex2:=evalf(int(gg(x),x = 0 .. Pi/4));

> for j from 100 to 500 by 50 do
tmp:=abs((valex2-rectangle(0,Pi/4,j,gg))/(valex2-rectangle(0,Pi/4,(j-50),gg)));
evalf(ln(tmp)/ln(abs((j-50)/j)) );
od;