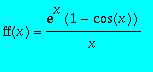
TD N°6 d'après les contrôles 2001
Exercices simples
Définir la fonction ff telle que pour x, on ait
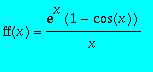
> ff:=x->exp(x)*(1-cos(x))/x;
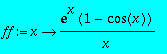
Définir la fonction, notée ff1, dérivee de ff.
> ff1:=D(ff);
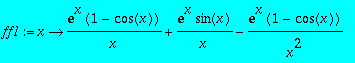
Définir la suite de listes de la forme [n/2,ff(n/2)], pour n=1 à 6.
> res:=seq([n/2,ff(n/2)],n=1..6);
![res := [1/2, 2*exp(1/2)*(1-cos(1/2))], [1, exp(1)*(...](images/td64.gif)
![res := [1/2, 2*exp(1/2)*(1-cos(1/2))], [1, exp(1)*(...](images/td65.gif)
Tracer sur le même graphe la suite de points définie à la question précédente ainsi que ff(x) pour x entre 0 et 3.
> plot({[res],ff(x)},x=0..3);
![[Maple Plot]](images/td66.gif)
Calculer
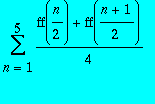 , donner une valeur approchée.
, donner une valeur approchée.
> evalf(sum((ff(n/2)+ff((n+1)/2))/4,n=1..5));
![]()
Calculer
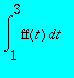 , donner une valeur approchée. Expliquer la relation d'ordre entre ce résultat et celui obtenu à la question précédente.
, donner une valeur approchée. Expliquer la relation d'ordre entre ce résultat et celui obtenu à la question précédente.
> evalf(int(ff,1/2..3));
![]()
Mécanique
On considère une masse assujettie à se déplacer sur l'axe 0x, m reliée à un ressort de constante de raideur k et soumis à un frottement fluide -fv(t). On prendra k/m=1 et f/m=1. Initialement la masse est au repos. Entre t=0 et t=1 la masse recoit une force d'amplitude A, dirigée vers les x positifs. (On prend A/m=1). L'équation du mouvement peut s'écrire

Tracer
![]() entre les instants t=-1 et t=5.
entre les instants t=-1 et t=5.
Résoudre l'équation du mouvement. Tracer la solution x(t) en fonction de t entre 0 et 10.
> plot(Heaviside(t)-Heaviside(t-1),t=-1..5);
![[Maple Plot]](images/td613.gif)
> res:=simplify(dsolve({diff(x(t),t$2)+x(t) = Heaviside(t)-Heaviside(t-1),x(0)=0,D(x)(0)=0},x(t)));
![]()
Pour voir le résultat plus simplement.
> convert(res,piecewise);
![x(t) = PIECEWISE([0, t < 0],[undefined, t = 0],[-co...](images/td615.gif)
> plot(rhs(res),t=0..10);
![[Maple Plot]](images/td616.gif)
Dans une seconde expérience la masse recoit une force constante d'amplitude A entre t=0 et t=1, puis à nouveau la même force entre t=3 et t= 4.
Donner l'équation différentielle du mouvement, résoudre cette équation et tracer x(t) en fonction de t.
>
res2:=simplify(dsolve({diff(x(t),t$2)+x(t) = Heaviside(t)-Heaviside(t-1)+Heaviside(t-3
)-Heaviside(t-4),x(0)=0,D(x)(0)=0},x(t)));
![]()
![]()
![]()
> convert(res2,piecewise);
![x(t) = PIECEWISE([0, t < 0],[undefined, t = 0],[-co...](images/td620.gif)
> plot({rhs(res2)},t=-2..20);
![[Maple Plot]](images/td621.gif)
Dans une troisieme expérience la masse recoit une force entre t=0 et t=1, puis à nouveau une force entre t=Pi et t= Pi+1.
Donner l'équation différentielle du mouvement. résoudre cette équation et tracer x(t) en fonction de t.
> res3:=simplify(dsolve({diff(x(t),t$2)+x(t) = Heaviside(t)-Heaviside(t-1)+Heaviside(t-Pi)-Heaviside(t-Pi-1),x(0)=0,D(x)(0)=0},x(t)));
![]()
![]()
![]()
> convert(res3,piecewise);
![x(t) = PIECEWISE([0, t < 0],[undefined, t = 0],[-co...](images/td625.gif)
> plot({rhs(res3)},t=-2..20);
![[Maple Plot]](images/td626.gif)
Tracer les trois solutions obtenues sur un même graphe. Commenter le résultat obtenu.
> plot([rhs(res3),rhs(res2),rhs(res)],t=-2..20);
![[Maple Plot]](images/td627.gif)
Démonstration sous Maple.
On cherche à montrer la formule suivante
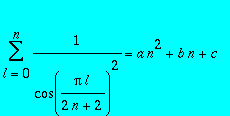 , où a, b et c sont des nombres rationnelles que l'on va déterminer.
, où a, b et c sont des nombres rationnelles que l'on va déterminer.
Définir une fonction de la variable n qui calcule la somme de l'équation définie ci-dessus.
> tt:=n->sum(1/(cos(Pi*l/(2*n+2)))^2,l=0..n);;
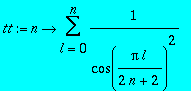
Calculer
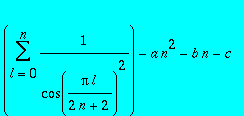 =0, pour n de 1 à 3. Résoudre ce système de trois équations pour les trois inconnus. Utiliser l'instruction convert avec l'option radical pour simplifier les expressions.
=0, pour n de 1 à 3. Résoudre ce système de trois équations pour les trois inconnus. Utiliser l'instruction convert avec l'option radical pour simplifier les expressions.
Calculer
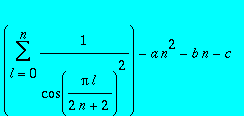 =0, pour n de 2 à 4. Résoudre ce nouveau système de trois équations. Commenter
=0, pour n de 2 à 4. Résoudre ce nouveau système de trois équations. Commenter
Faire une boucle for pour calculer de manière approchée
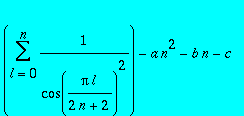 , avec les valeurs de a, b et c précédement déterminées pour n=5 a 15. Conclusion.
, avec les valeurs de a, b et c précédement déterminées pour n=5 a 15. Conclusion.
Même exercice avec la somme
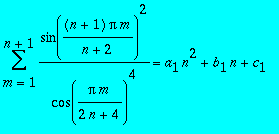
> suit:=seq(convert(tt(i),radical)-a-b*i*i-c*i,i=1..3);
![]()
> suit2:=seq(convert(tt(i),radical)-a-b*i*i-c*i,i=2..4);
![]()
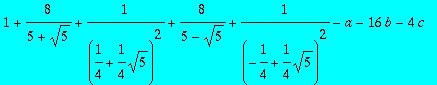
> solve({suit});
![]()
> solve({suit2});
![]()
> for i from 5 to 15 do evalf(tt(i)-1-4/3*i-2/3*i*i)od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
>
Les quinze valeurs sont nulles à la précision du calcul. Sans que cela soit une preuve, c'est une très bonne indication pour que la propriété soit vraie
> tt2:=n->sum(sin((n+1)*Pi*m/(n+2))^2/(cos(Pi*m/(2*n+4))^4),m = 1 .. n+1);
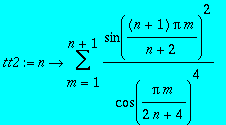
> suit3:=seq(convert(tt2(i),radical)-a-b*i-c*i*i,i=1..3);
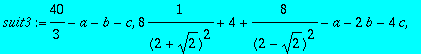
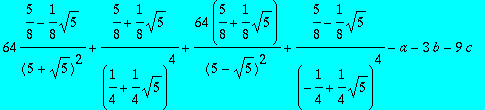
> solve({suit3});
![]()
> suit4:=seq(convert(tt2(i),radical)-a-b*i-c*i*i,i=2..4);
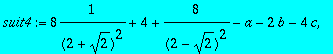
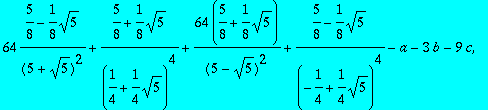
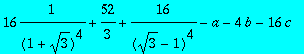
> solve({suit4});
![]()
> for i from 5 to 15 do evalf(tt2(i)-4-20/3*i-8/3*i*i)od;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
>
Même conclusion.