TD 3 Eléments de programmation, suites numériques et fonction Zeta

I. Les instructions conditionnelles et les boucles

Pour exécuter des instructions répétitives sur une suite de valeurs repérées par un indice, on a la structure suivante :

for i from début by pas to fin

do
suite d'instructions ;
od ;

Exemple

> somme:=0;for i from 1 to 10 do somme:=somme+i*i;od;

Veuillez noter la syntaxe de l'exemple donné ci-dessus. Que se passe-t-il quand on remplace la dernière ligne par od :

Les nombres de Fibonacci sont définis par la relation de récurrence suivante

F0=0 F1=1 Fn=Fn-1+Fn-2 pour n>2
Calculer avec une boucle for les valeurs de F3 à F10.

Rappel: || est l'opérateur de concaténation et peut être utilisé pour définir des variables successives dans une boucle.

> F0:=0;F1:=1;

> for i from 2 to 10 do F||i:=F||(i-1)+F||(i-2);od;

>

La boucle while:

Pour répéter une séquence d'instructions tant qu'une condition est vraie, on a la structure suivante :

while condition

do
suite d'instructions ;
od ;

En reprenant l'exemple des nombres de Fibonacci déterminer la plus grande valeur de n telle que Fn<200.

> F0:=0;F1:=1;i:=1;

> i:=1;while (F||i < 200) do F||(i+1):=F||i+F||(i-1);print(i,F||i);i:=i+1;od:

Les instructions conditionnelles sont définies par la séquence suivante
if condition then
suite d'instructions 1 ;
else
suite d'instructions 2 ;
fi ;
Si la condition est vraie, la suite d'instructions 1 est exécutée, sinon la suite d'instructions 2 l'est.
Dans le cas où une séquence de choix est supérieure à 2, la syntaxe est la suivante
if condition then
suite d'instructions 1 ;
elif condition2 then
suite d'instructions 2 ;
elif condition3 then
suite d'instructions 3 ;
…
else
suite d'instructions n
fi ;

II Les procédures

Nous avons un moyen de définir des fonctions simples.

Par exemple, f := x-> ; définit une fonction f qui pour toute valeur de x associe la valeur .

Il est parfois nécessaire de définir des fonctions comprenant des instructions conditionnelles et/ou des boucles.

La structure d'une procédure est la suivante :

proc (suite de variables)
local suite de variables locales ;
options suite d'options ;
instruction1 ;
instruction2 ;
¯
instruction n ;
end ;

L'instruction local permet de définir des variables durant le temps de l'exécution de la procédure et qui disparaissent une fois la procédure terminée. Cette instruction n'est présente que si des variables supplémentaires sont nécessaires à l'exécution de la procédure.
Reprenons la fonction donnée ci-dessus, on a alors la suite d'instructions suivantes
f:=proc(x)
;
end;

Pour les nombres de Fibonacci, on peut définir la procédure suivante

> Fib:=proc(n::nonnegint)
if n=0 then 0

> elif n=1 then 1

> else Fib(n-1)+Fib(n-2)fi
end ;

La directive negposint signifie que la procédure n'accepte comme variables d'entrée que des nombres entiers positifs ou nuls.

Attention, cette fois-ci Fib est une procédure et non pas une suite de nombres comme dans l'exemple précédent.

Calculer Fib(30) à partir de cette procédure. Que remarque-t-on ?
Ajouter l'option remember dans la procedure et calculer Fib(40).

> Fib(10);

> Fib:=proc(n::nonnegint)
option remember;
if n=0 then 0

> elif n=1 then 1

> else Fib(n-1)+Fib(n-2)fi
end ;

> Fib(40);

Ecrire une procédure qui définit les polynômes de Legendre qui satisfont la relation de récurrence suivante
,

=((2n-1) -(n-1) )/n

> Leg:=proc(n::nonnegint,x)
option remember;

> if n=0 then 1

> elif n=1 then x

> else expand(((2*n-1)*x*Leg(n-1,x)-(n-1)*Leg(n-2,x))/n) fi

> end;

> Leg(12,x);

>

En utilisant la bibliothèque des polynomes orthogonaux, vérifier les résultats obtenus sur les polynomes de Legendre.

> with(orthopoly):

> P(12,x);

III Suites numériques

Pour une fonction , on considère la suite définie par et
Soit

Definissez les 10 premières valeurs de l'aide d'une boucle. Rangez les valeurs dans x.i pour i=1 à 10.

> FF:=x->x^2+0.1875;

> x0:=-0.5;

> for i from 1 to 10 do

> x||i:=(FF(x||(i-1)));

> od;

Visualisation de la convergence de la suite.
La liste de points à construire dans cet exercice est de la forme . On souhaite aussi tracer le graphe y=FF(x), la suite ainsi que la diagonale y=x. en utilisant la commande plot . Pour déterminer la fenêtre de visualisation, on calculera la plus grande valeur et la plus petite valeur de la suite des x avec les instructions min et max .

> res:=seq(op([[x||i,x||i],[x||i,x||(i+1)]]),i=0..9);

> xmin:=min(seq(x||i,i=0..9));xmax:=max(seq(x||i,i=0..9));

> plot([[res],FF(x),x],x=xmin..xmax,color=[blue,red,green]);

Créer une procédure dessin dont les variables d'entrée seront le nombre de points, la condition initiale , le nom de la fonction et dont la sortie sera un graphique. Tester cette procédure pour les conditions intiales suivantes: en premier =0, puis =-0.5

> dessin:=proc(n,y,f)

> local x0,i,res,xmin,xmax;

> x||0:=y;

> for i from 0 to n-1 do x||(i+1):=f(x||i); od;
xmin:=min(seq(x||i,i=0..n));
xmax:=max(seq(x||i,i=0..n));

> res:=seq(op([[x||i,x||i],[x||i,x||(i+1)]]),i=0..n-1);

> plot([[res],f(x),x],x=xmin..xmax,color=[blue,red,green]);

> end;

> dessin(10,0.3,FF);

> dessin(10,-0.5,FF);

En utilisant la procédure dessin, visualiser les suites pour la fonction pour les conditions initiales =-0.7 et =-1.618

> FF1:=x->1-x^2;

> dessin(20,0.6,FF1);

> dessin(20,-1.618,FF1);

IV Programmation évoluée: affectation multiple, apprendre à copier, modules...

Une possibilité intéressante de Maple est de permettre les affectations simultanées L'opérateur correspondant est la paire de parenthèses.

Par ex: a1:=9; a2:=13;;
(a1,a2):=(a2,a1);
Vérifier la valeur de chacune des variables après cette opération.

Soit maintenant les variables a3:=6;a4:=-7;

Donner en une ligne l'instruction qui affecte la valeur de a4 à a1, de a3 à a2, a1 à a3 et a2 à a4.

Vérifier le résultat. Commenter.

Une façon politiquement incorrecte pour apprendre à programmer consiste à copier ce que vos brillants prédécesseurs ont fait. (Cela peut vous laisser rêveur pour les concours!). Maple permet et encourage ce type de pratique, qui est très utile pour progresser rapidement.

L'instruction interface(verboseproc=2) associée à l'instruction eval vous permet de connaître la manière dont les instructions de Maple sont écrites.

Ecrire:

interface(verboseproc=2);

with(combinat);

eval(fibonacci);

Afficher le code Maple pour les nombres de Bernouilli.

>

Les modules sont un ensemble de procédures avec la notion de variables à exporter et la notion de variables locales.

Ex:

> fonc:=module()

> export integre,suite,trace;

> suite:=proc(n,a,b,f) local i;

> seq(f(a+i*(b-a)/n),i=0..n);

> end;

> integre:=proc(a,b,f)

> int(f(x),x=a..b);

> end;
trace:=proc(a,b,f) plot(f,a..b) end;

> end module;

> FF:=x->x^2+1;

> fonc:-integre(0,1,FF);

> fonc:-suite(10,0,1,FF);

> fonc:-trace(0,1,FF);

V.La fonction Zeta et la conjecture de Riemann

La fonction Zeta est définie comme 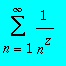pour i allant de 1 à l'infini pour toute valeur de z

telle que Re(z>1).

Un prolongement analytique permet en fait de prolonger cette fonction pour toute valeur de z

complexe différente de 1. Riemann a montré que Zeta(-2*n) s'annule pour tout entier n

strictement positif et a conjecturé que les autres zéros de Zeta sont tous situés sur

l'axe z=1/2+iy, appelé ligne critique. Depuis la preuve du théorème de Fermat en 1995

par Wiles, la conjecture de Riemann reste l'un des problèmes mathématiques importants

non résolus.

Tracer le module de la fonction Zeta entre 0 et 60 le long de la ligne critique.

> plot(abs(Zeta(1/2+y*I)),y=0..56,numpoints=200);

Calculer en utilisant une boucle tous les zéros entre 0 et 60 le long de la ligne critique.

> j:=0;for i from 12 to 60 do res:=fsolve(abs(Zeta(1/2+y*I)),y=i..i+1);if type(res,realcons) then zero||j:=res; print(zero||j);j:=j+1; fi;od:print(j-1);