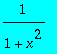TD 11 Développement limité, notion de rayon de convergence ,

et approximants de Padé

I Développement limité

En utilisant l'instruction taylor , faire le développement limité de l'expression 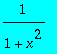, à l'ordre 6 en x

> devel:=taylor(1/(1+x^2),x,7);

A partir de l'instruction convert avec l'option polynom , tracer l'expression de ci-dessus et le polynôme de degré 6 obtenu pour x compris entre -2 et 2 et pour y compris entre -2 et 2.

> pol6:=convert(devel,polynom);

> plot([1/(1+x^2),pol6],x=-2..2,y=-2..2);

En utilisant l'instruction seq ou une boucle , déterminer les polynômes correspondants à des développements limités de l'ordre 2 jusqu'à l'ordre 32. Tracer un graphe contenant 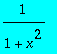et les développements jusqu'à l'ordre 16, puis un second graphe contenant 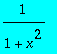et les développements de l'ordre 18 à 36,

> pols:=seq(convert(taylor(1/(1+x^2),x,2*i+1),polynom),i=1..16);

> plot([1/(1+x^2),pols[1..8]],x=-2..2,y=-2..2);

> plot([1/(1+x^2),pols[9..16]],x=-2..2,y=-2..2);

Que remarque-t-on? Que se passe-t-il quand on inclut de plus en plus d'ordres dans le développement limité? Quel est le rayon de convergence de la série?

En incluant des ordres de plus en plus élevés, l'expression est de mieux en mieux approximé dans l'intervalle de -1 à 1, mais au voisinage des extrémités de l'intervalle le développement limité tend vers une grandeur très grande positive ou négative. Le rayon de convergence de la série semble être de 1.

On considère maintenant la fonction 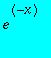. Reprendre les questions précédentes. Pour le graphe contenant les développements de l'ordre 18 à 36, on tracera les courbes pour x compris entre 0et 10.

> pols3:=seq(convert(taylor(exp(-x),x,i),polynom),i=1..36):

> plot([exp(-x),pols3[1..15]],x=0..10,y=0..2);

> plot([exp(-x),pols3[16..20]],x=0..10,y=0..2);

> plot([exp(-x),pols3[30..36]],x=0..15,y=0..2);

On voit graphiquement que l'exponentielle est bien approximée par un développement à l'ordre n sur un intervalle de -n a +n. Sans que cela soit une démonstration, on peut supposer que le rayon de convergence est infini, ce qui se démontre proprement par ailleurs.

>

II Padé

Un approximant de Padé [m,n ] est une fraction rationnelle d'un polynôme de degré m sur un polynôme de degré n qui approxime la fonction telle que son développement limité soit exact à l'ordre n+m. L'instruction s'appelle pade (voir la page d'aide).

Tracer sur une même courbe le développement limité d'ordre 6 pour x=0 de exp(-x), tous les padés possibles et la courbe elle-même.

> with(numapprox):

> PADE:=seq(pade(exp(-x),x,[i,6-i]),i=0..6);

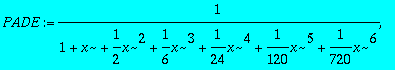
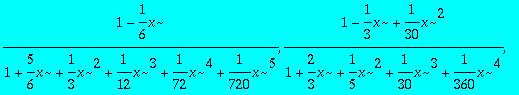
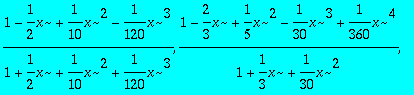
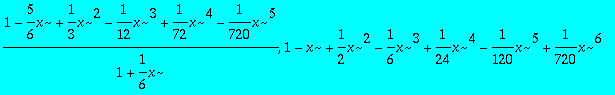
> devel:=convert(taylor(exp(-x),x,7),polynom);

> plot({exp(-x),devel,PADE},x=0..8,color=[red,black,yellow]);

A l'aide de l'instruction infnorm , déterminer le meilleur approximant de l'exponentielle dans l'intervalle [0,2], puis [0,8]

> for i from 0 to 6 do FPAD||i:=unapply(PADE[i+1],x) od:

> for i from 0 to 6 do toto:=infnorm(1/exp-FPAD||i,0..2);print(toto,i);od;

>

> for i from 0 to 6 do toto:=infnorm(1/exp-FPAD||i,0..2);print(toto,i);od;

Tracer sur une même courbe le développement limité d'ordre 6 pour x=0 de 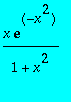, tous les padés possibles et la courbe elle-même

> PADE2:=seq(pade(exp(-x^2)/(1+x^2),x,[2*i,6-2*i]),i=0..3);

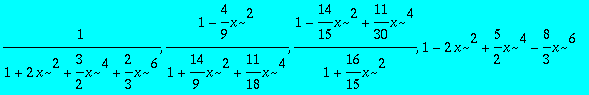
> devel2:=convert(taylor(x*exp(-x^2)/(1+x^2),x,7),polynom);

> plot({exp(-x^2)/(1+x^2),devel2,PADE2},x=-2..2,y=-4..4,color=[red,black,yellow]);

>

A l'aide de l'instruction infnorm , déterminer le meilleur approximant de l'exponentielle dans l'intervalle [-2,2]. Que peut-on dire par rapport au dévelopement limité?

> for i from 0 to 3 do FPAD2||i:=unapply(PADE2[i+1],x) od:

> myfunc:=unapply(exp(-x^2)/(1+x^2),x);

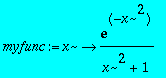
> for i from 0 to 3 do toto:=infnorm(myfunc-FPAD2||i,-2..2);print(toto,i);od;