TD 10 Hydrostatique et diffusion de la chaleur
.
Hydrostatique
On considère un fluide isotherme en équilibre soumis à un champ de pesanteur uniforme. Ecrire l'équation de l'hydrostatique. On considère que le gaz est parfait c'est à dire que
![]() . Résoudre simultanément l'ensemble des équations (hydrostatique et équation d'etat). Sachant que pour z=0, la pression est ; Tracer
. Résoudre simultanément l'ensemble des équations (hydrostatique et équation d'etat). Sachant que pour z=0, la pression est ; Tracer
![]() et
et
![]() en fonction de z pour
en fonction de z pour
![]() =0.7,
=0.7,
![]() et
et
![]() = 1.
= 1.
> ehy:=diff(P(z),z)+m*g*rho(z);
![]()
> etat:=P(z)=k[B]*T*rho(z);
![]()
> resh:=dsolve({ehy,etat,rho(0)=0.7},{rho(z),P(z)});
![resh := {P(z) = 7/10*k[B]*T*exp(-m/T*g/k[B]*z), rho...](images/td109.gif)
> rgp:=[subs(m=k[B]*T/g,rhs(resh[1])/(k[B]*T)),subs(m=k[B]*T/g,P[0]=0.7,rhs(resh[2]))];
![]()
> plot(rgp[1],z=0..5);
![[Maple Plot]](images/td1011.gif)
On considère maintenant que les particules ont une taille finie. L' équation d'état exacte à une dimension est donnée par
![P(z) = k[B]*T*rho(z)/(1-rho(z))](images/td1012.gif) . Reprendre les questions précédentes.
. Reprendre les questions précédentes.
> ehy:=diff(P(z),z)+m*g*rho(z);
![]()
> etat2:=P(z)=k[B]*T*rho(z)/(1-rho(z));
![etat2 := P(z) = k[B]*T*rho(z)/(1-rho(z))](images/td1014.gif)
> resh2:=dsolve({ehy,etat2,rho(0)=0.7},{rho(z),P(z)});
![resh2 := {rho(z) = k[B]*T*LambertW(1/k[B]/T*exp(-m/...](images/td1015.gif)
![resh2 := {rho(z) = k[B]*T*LambertW(1/k[B]/T*exp(-m/...](images/td1016.gif)
> rr:=subs(m=k[B]*T/g,k[B]=1/T,rhs(resh2[2]));
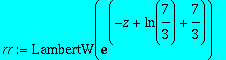
> pp:=subs(m=k[B]*T/g,k[B]=1/T,rhs(resh2[1]));
>
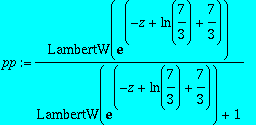
> plot([pp,rr],z=0..5);
![[Maple Plot]](images/td1019.gif)
Tracer les courbes
![]() pour le gaz parfait et le gaz réel sur un même graphe. De même pour P(z). Conclusion
pour le gaz parfait et le gaz réel sur un même graphe. De même pour P(z). Conclusion
> plot({rgp[1],rr},z=0..5);
![[Maple Plot]](images/td1021.gif)
> plot([rgp[2],pp],z=0..5);
![[Maple Plot]](images/td1022.gif)
Diffusion de la chaleur
On considre un milieu homogène la température est
![]() au temps
t=0
compris entre
x=a
et
x=b
dont la diffusivité de chaleur est
au temps
t=0
compris entre
x=a
et
x=b
dont la diffusivité de chaleur est
![]() . Ce mileu est mis en contact avec un thermostat à la temprature
. Ce mileu est mis en contact avec un thermostat à la temprature
![]() au point x=a. On désigne par
au point x=a. On désigne par
![]() la tempraure l'abscisse
x
et l'instant
t
. En l'absence de source de chaleur, le champ
la tempraure l'abscisse
x
et l'instant
t
. En l'absence de source de chaleur, le champ
![]() obéit à l'équation de la chaleur :
obéit à l'équation de la chaleur :
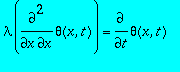 .
.
Ecrire une procédure (ou une fonction) qui à une fonctionapplique l'équation différentielle précédente
> eq:=theta->lambda*diff(theta(x,t),x,x) = diff(theta(x,t),t):
Mur semi-infini. On prend ici
a=0
et
![]() .Recherche des solutions de la forme
f(u)
avec
.Recherche des solutions de la forme
f(u)
avec
![]() . Quels sont les couples (
. Quels sont les couples (
![]() ) possibles. Insérer la fonction
) possibles. Insérer la fonction
![]() dans l'équation différentielle, puis faire apparaître
u
par
dans l'équation différentielle, puis faire apparaître
u
par
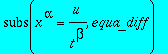 . Choisir (
. Choisir (
![]() ) pour que le résultat ne dépende que de
u
) pour que le résultat ne dépende que de
u
>
f:='f':F:=(x,t)->f(x^alpha*t^beta);
eq(F);
expand(subs(x^alpha = u/(t^beta), eq(F)*x^2/(u*D(f)(u))));
![]()
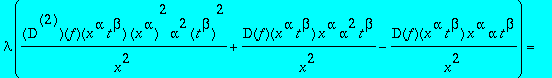
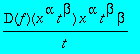
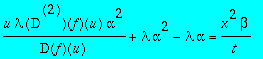
![]()
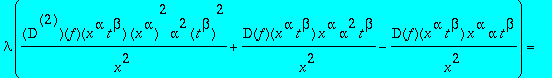
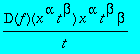

Déterminer l'équation différentielle pour f(u), lorsque
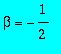 . Résoudre pour les conditions initiales données dans l'introduction
. Résoudre pour les conditions initiales données dans l'introduction
>
assume(t>0,u>0,x>0,lambda>0):
eq(F);equ:=simplify(subs(x = u*sqrt(t),beta=-1/2,alpha=1, eq(F)*t));
![]()
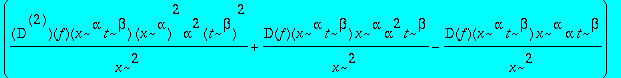
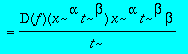
![]()
> f1:=subs(alpha=1,beta=-1/2,f);
>
![]()
> sol:=collect(dsolve({equ,f(0)=Theta[1],f1(infinity)=Theta[0]},f(u)),erf);
![]()
Tracez
![]() pour
pour
![]() ,
,
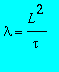 en posant
en posant
![]() et
et
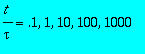
> assume(L>0,tau>0);f2:=simplify(subs(u=x/sqrt(t),Theta[0] = 0, Theta[1] = 100, x = X*L, lambda=L^2/tau , t=mu*tau,rhs(sol)));
![]()
> plot([seq(f2,mu=( .1,1,10,100,1000))],X=0..10);
![[Maple Plot]](images/td1056.gif)
Diffusion de la chaleur dans un mur d'épaisseur
a
compris entre
x=0
et
x=a
.On recherche ici les solutions particulières de la forme
![]()
Montrer que
 = b[n]*sin(n*Pi*x/a)*exp(-t/tau[n])](images/td1058.gif) est une solution particulière pour
est une solution particulière pour
![tau[n] = tau[1]/(n^2)](images/td1059.gif) , et donner
, et donner
![]() . Pourquoi
n
doit-il être entier?
. Pourquoi
n
doit-il être entier?
>
fn:=(x,t)->b[n]*sin(n*Pi*x/a)*exp(-t/tau[n]);
eqd:=eq(fn);eqtau:=rhs(eqd)/lhs(eqd);
Tau[1]:=solve(subs(tau[n]=tau[1]/n^2,eqtau)=1,tau[1]);
>
![fn := proc (x, t) options operator, arrow; b[n]*sin...](images/td1061.gif)
![eqd := -lambda*b[n]*sin(n*Pi*x/a)*n^2*Pi^2/a^2*exp(...](images/td1062.gif)
![eqtau := 1/tau[n]/lambda/n^2/Pi^2*a^2](images/td1063.gif)
![Tau[1] := a^2/lambda/Pi^2](images/td1064.gif)
On recherche maintenant la solution du problème sous la forme
,n = 0 .. infinity)](images/td1065.gif)
Exprimer
![]() en fonction de
en fonction de
![]()
> theta(x,0)=sum(fn(x,0),n=0..infinity);
![theta(x,0) = sum(b[n]*sin(n*Pi*x/a),n = 0 .. infini...](images/td1068.gif)
Calculer les
![]() sachant que
sachant que
![]() pour x compris entre 0 et a
et
pour x compris entre 0 et a
et
![]() en dehors de cet intervalle
en dehors de cet intervalle
>
assume(m,integer):assume(n,integer);
eqb:=int((Theta[0]-Theta[1])*sin(n*Pi*x/a),x=0..a)=int(b[n]*sin(n*Pi*x/a)*sin(n*Pi*x/a),x=0..a);
B:=unapply(solve(eqb,b[n]),n);
![eqb := a*(Theta[1]-Theta[0])*((-1)^n-1)/n/Pi = 1/2*...](images/td1072.gif)
![B := proc (n) options operator, arrow; 2*(Theta[1]*...](images/td1073.gif)
> simplify([B(2*n),B(2*n+1)]);
![[0, -4*(Theta[1]-Theta[0])/(2*n+1)/Pi]](images/td1074.gif)
Tracer la fonction
![]() lorsque la somme est tronquée à 10 termes, 20 termes, 100 termes
lorsque la somme est tronquée à 10 termes, 20 termes, 100 termes
> i:='i';theta[approx]:=unapply(sum(B(i)*sin(i*Pi*x/a),i=1..n),x,n);
![]()
![theta[approx] := proc (x, n) options operator, arro...](images/td1077.gif)
> plot([seq(simplify(theta[approx](a*x,k)/(Theta[0]-Theta[1])),k=(10,20,100))],x=0..1,color=[red,green,blue]);
![[Maple Plot]](images/td1078.gif)
Définir la fonction
![]() pour une somme tronquée à 10 termes. Utiliser les variables sans dimension X=ax et
pour une somme tronquée à 10 termes. Utiliser les variables sans dimension X=ax et
![T = t/tau[1]](images/td1080.gif)
> theta[approxt]:=(X,T,n)->(sum(simplify(B(i)/(Theta[0]-Theta[1]))*sin(i*Pi*X)*exp(-T*i^2),i=1..n));
![theta[approxt] := proc (X, T, n) options operator, ...](images/td1081.gif)
> theta[approxt](x,t,10);
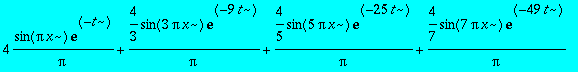
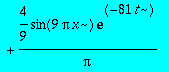
Tracer cette fonction pour
![t/tau[1] = 10^k](images/td1084.gif) pour k entier de -4 à 0. Que se passe-t-il lorsque le nombre de termes passe 20 puis 100?
pour k entier de -4 à 0. Que se passe-t-il lorsque le nombre de termes passe 20 puis 100?
>
![]()
![]()
![[Maple Plot]](images/td1087.gif)
>
![]()
![]()
![[Maple Plot]](images/td1090.gif)
>
![]()
![]()
![[Maple Plot]](images/td1093.gif)
>
![]()
![]()
![[Maple Plot]](images/td1096.gif)
Comment varie la température en
![]() ? Tracer les variations.
? Tracer les variations.
> (theta[approxt](1/2,t,20));
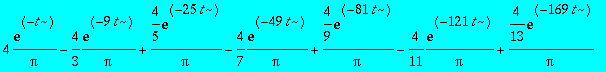
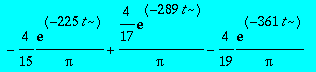
> plot([seq(theta[approxt](1/2,t,n),n=(10,20,100))],t=0..0.1,color=[red,green,blue]);
![[Maple Plot]](images/td10100.gif)
> plot([seq(theta[approxt](1/2,t,n),n=(10,20,100))],t=0..5,color=[red,green,blue]);
![[Maple Plot]](images/td10101.gif)
>
>