TD 1 Introduction à Maple
Bref aperçu des possibilités de Maple
Taper, par exemple 2+8; puis à la ligne 3/7+8/17;
> 2+8;
![]()
> 3/7+8/17;
![]()
Remarque : Maple donne le résultat exact. Pour une valeur approchée décimale, on doit taper
> evalf(3/7+8/17);
![]()
Par défaut, Maple fournit 10 chiffres. Il est possible de modifier cette valeur en tapant l'instruction
> Digits:=20;
![]()
Exécuter à nouveau l'instruction d'évaluation numérique pour 3/7+8/17
> evalf(3/7+8/17);
![]()
Un certain nombre de constantes mathématiques sont prédéfinies. Le nombre pi s'écrit Pi.
En utilisant l'instruction evalf et Digits, afficher les 100 premières décimales de Pi.
> Digits:=100;evalf(Pi);
![]()
![]()
![]()
Calculer Pi^(Pi^Pi) avec 15 décimales;
Taper sqrt(2*sqrt(19549)+286);
> Digits:=15;evalf(Pi^(Pi^Pi));
![]()
![]()
> sqrt(2*sqrt(19549)+286);
![]()
Factoriel d'un nombre
Calculer6!;69 !234 !
Décomposition en facteurs premiers; en utilisant l'instruction
ifactor
, calculer la décomposition de 123 et de factoriel 56.
> 6!;69!;
![]()
![]()
![]()
> 234!;
![]()
![]()
![]()
![]()
![]()
![]()
Opérations sur les polynômes: développement et factorisation.On peut développer une expression mathématique avec l'instruction expand . Développer
le polynôme 3*x^2+7*x-4)^4.
Inversement, on peut factoriser avec l'instruction factor . Effectuer cette opération sur le polynôme 81x^8 - 432x^6 + 864x^4 - 768x^2 + 256.
> expand((3*x^2+7*x-4)^4);
![]()
> factor(81*x^8 - 432*x^6 + 864*x^4 - 768*x^2 + 256);
![]()
Calcul différentiel et intégral sous Maple.
Pour calculer la dérivée première de x^6 par rapport à x, on utilise l'instruction diff
diff(x^6,x);
Pour la dérivée seconde
diff(x^6,x$2);
Calculer la dérivée sixième de exp(-x^2) ;
> diff(exp(-x^2),x$6);
![]()
Pour calculer la primitive d'une fonction, on utilise l'instruction
int
int(t^5*exp(-t),t);
Pour calculer l'intégrale, on utilise aussi l'instruction
int
int(t^5*exp(-t),t=0..1);
Calculer int(t^6/(1+t^8),t=0..infinity);
> int(t^6/(1+t^8),t=0..infinity);
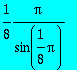
Module graphique de Maple.
Pour tracer une expression de type y=f(x) dans un intervalle de x donné, on utilise l'instruction plot .
> plot(cos(x)*exp(-x/2),x=0..4);
![[Maple Plot]](images/td125.gif)
Pour tracer une surface du type z=f(x,y) on utilise l'instruction plot3d
> plot3d(sin(v)*sin(w),v=-Pi..Pi,w=-Pi..Pi);
![[Maple Plot]](images/td126.gif)
Quelques définitions
Expression
Le résultat d'une expression peut avoir un nom et être utilisé dans la suite des calculs.
La syntaxe est la suivante
nom:=instruction;
Exemple
A1:=89 ;B1:=17 ;
> C1:=A1+B1 ;
![]()
![]()
![]()
Exemple 2
>
A1:=x+9 ;
A1^2+C^3 ;
![]()
![]()
Composition d'instructions.
Une instruction de Maple doit être terminée soit par un ; soit par un : suivie de la touche entrée afin d'être exécutée. Dans le premier cas, il y a affichage du résultat, alors qu'il n'y en a pas dans le second cas.
Pour lier un ensemble d'instructions entre elles, nous allons utiliser la méthode suivante
1) chaque instruction doit posséder un nom (contenant au moins deux lettres pour éviter de confondre avec les variables et les lettres réservées.).
2) Ecrire l'opération algébrique en utilisant les noms d'instructions.
Cette méthode peut paraître un peu lourde dans un premier temps, mais elle est nécessaire dès que le nombre d'instructions liées est supérieur à quelques unités.
Ex : P1:=(2*x^2-4*x+7) ;
P2 :=expand(P1*P1) ;
Réinitialisation des variables.
Taper Taper
x :=3 ;
P1 ;
P2 ;
Si on veut réinitialiser la variable x,
x :='x' ;
Taper à nouveau P1 ; P2 ;
Fonctions
Pour définir une fonction en Maple, il y a plusieurs possibilités
nom_de_fonction:=variable ->expression;
nom_de_fonction:=unapply(expression, variable);
Ne jamais mettre de parenthèses dans les noms de fonctions !
Définir en utilisant les deux définitions précédentes une fonction f telle que pour tout x, la fonction donne f(x)=x^3+2.
en utilisant chacune des deux possibilités.
Pour vérifier qu'une fonction est correctement définie, tapez f(y);
Posons à nouveau : P1=(2*x^2-4*x+7) ;
Essayer à partir de P1 les deux défintions pour définir une fonction g telle que g(x)=(2*x^2-4*x+7) ;
Conclusion.
> P1:=(2*x^2-4*x+7);
![]()
> P2 :=expand(P1*P1) ;
![]()
> x:=3;P1;P2;
![]()
![]()
![]()
> x :='x' ;P1 ; P2 ;
![]()
![]()
![]()
> f:=x->x^3+2;
![]()
> f(y);
![]()
> g:=unapply(x^3+2,x);
![]()
> g(t);
![]()
Composition de fonctions
Le caractère @ permet la composition de fonctions
Par exemple, pour calculer la fonctions fof, tapez
(f@f)(y)
Pour la composée 4ème, la syntaxe est
(f@@4)(t);
Calculer la 27ème dérivée de la composée 3ème de f.
> (f@f)(y);(f@@4)(t);
![]()
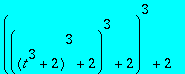
>
> diff((f@@3)(t),t$27);
![]()
Concours commun 2000 MP (extrait)
A partir d'un signal e(t)=Ecos(wt) et d'une porteuse haute fréquence p(t)=S sin(w0t) on génére le signal modulé
s(t)=S(1+ke(t))sin(w0t), porteur de l'information initiale, et qui sera transmis. On définit le taux de modulation par m=kE.
Tracer s(t) pour m<1 et m>1. On prendra S=1, w=1, w0=10, m=0.1, 0.5 et m=1.5
> plot((1+0.1*sin(t))*sin(10*t),t=0..20);
![[Maple Plot]](images/td147.gif)
> plot((1+0.5*sin(t))*sin(10*t),t=0..20);
![[Maple Plot]](images/td148.gif)
> plot((1+1.5*sin(t))*sin(10*t),t=0..20);
![[Maple Plot]](images/td149.gif)
En déduire qu'une détection d'enveloppe peut restituer l'information e(t) à une condition que l'on précisera.
A partir d'un signal e(t)=Ecos(wt) et d'une porteuse haute fréquence p(t)=S sin(w0t) on génére le signal modulé s(t)=sin(w0t+ke(t))), porteur de l'information initiale, et qui sera transmis. Tracer s(t) pour m=0.1 m=3.
> plot(sin(10*t+.1*sin(t)),t=0..20);
![[Maple Plot]](images/td150.gif)
> plot(sin(10*t+3*sin(t)),t=0..20);
![[Maple Plot]](images/td151.gif)
>