How to solve a sudoku puzzle using Monte Carlo simulation
A sudoku puzzle consists of a square grid of nxn blocks each containing
nxn cells. Typically, n=3. The puzzle is defined by a (variable) number
of integers in specified positions. The objective is to fill in
the remaining cells so that each row, column and block contains all
distinct integers from 1 to nxn once only.
Each block is examined and the open cells are filled with the remaining
integers, so each square contains all nine integers. The "energy"
is defined as 243 (3n4 in general) minus the sum of the
number of
unique elements in each row, column and block. When the puzzle is
solved, the energy is zero.
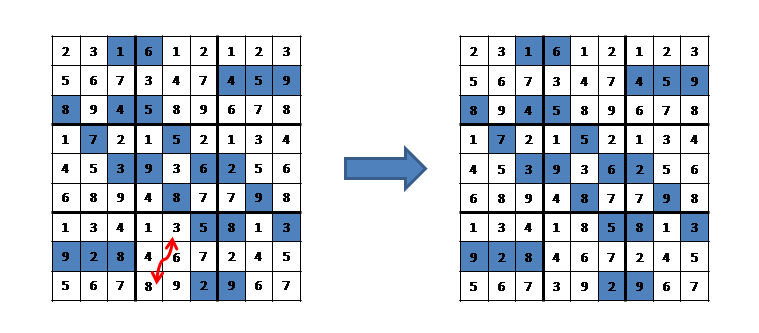
A Monte Carlo move consists of randomly selecting a pair of non-fixed
elements in a randomly selected block. These elements are then
exchanged to generate the trial configuration; see figure above. The
trial configuation
is then accepted or rejected using the standard Monte Carlo recipe.
That is, if exp(-(E(trial)-E)/T) < ξ, where ξ is a uniform
random number between 0 and 1, the trial configuration is
rejected. Otherwise it is accepted.
In simulated annealing the temperature is progressively lowered until
the system reaches the minimum energy configuration. In this
application, however, the solution can be found at a carefully chosen
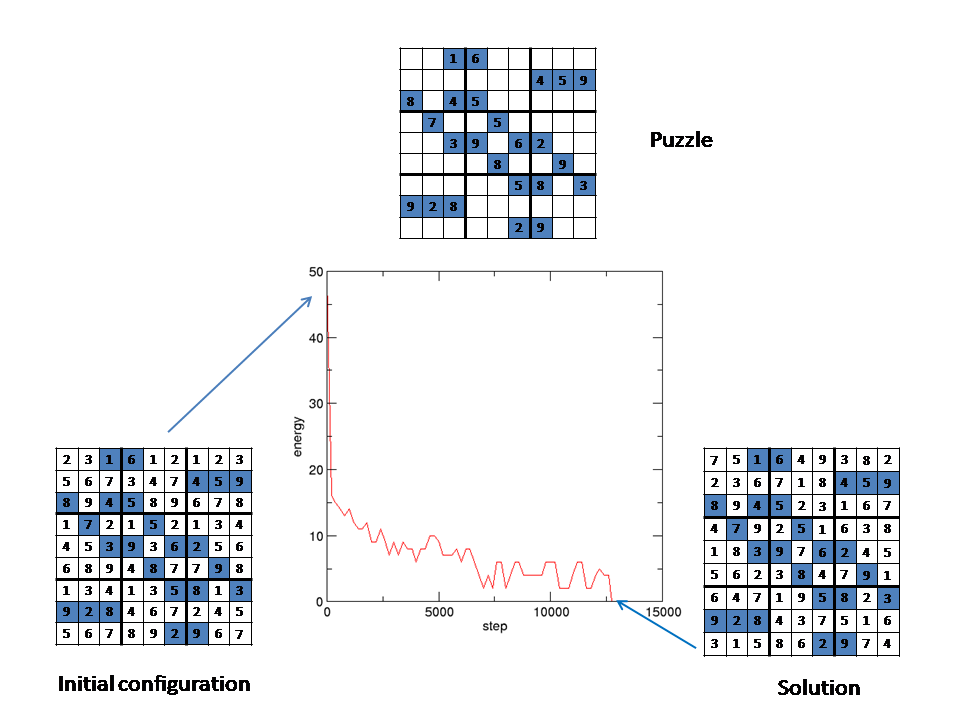
constant temperature. Here is what happens with a constant temperature
of 0.15. The solution, corresponding to energy=0, is found after
12741 steps.
On an Intel Core 2 Duo
processor, the calcuation takes less than one second.
Click to download the C program and a sample data file.
sudoku.c
sudoku.dat

