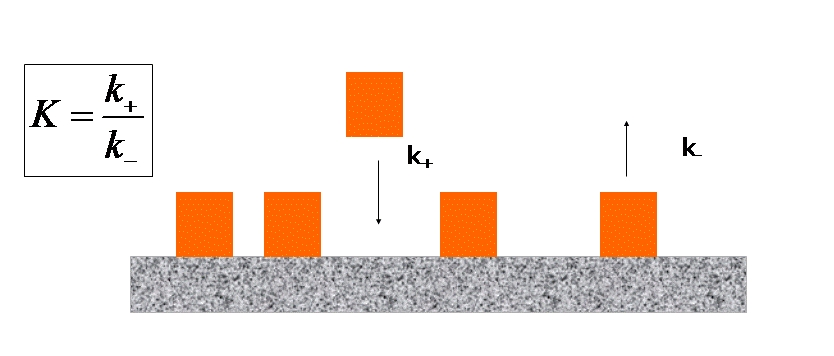
The Parking Lot Model
This model can describe the (reversible) adsorption of proteins,
as well as the compaction of a granular material subject to a sequence
of taps. The PLM can be defined in any dimension. Its realization
in
one-dimension
is a system of hard rods adsorbing and desorbing on a line of length L.
The rods
adsorb at a rate k+
and desorb at a rate k-. A rod can only
adsorb if it does not overlap with any other rod. If the
process starts from an empty
line, the density ρ = N/L increases until a steady state is
reached.
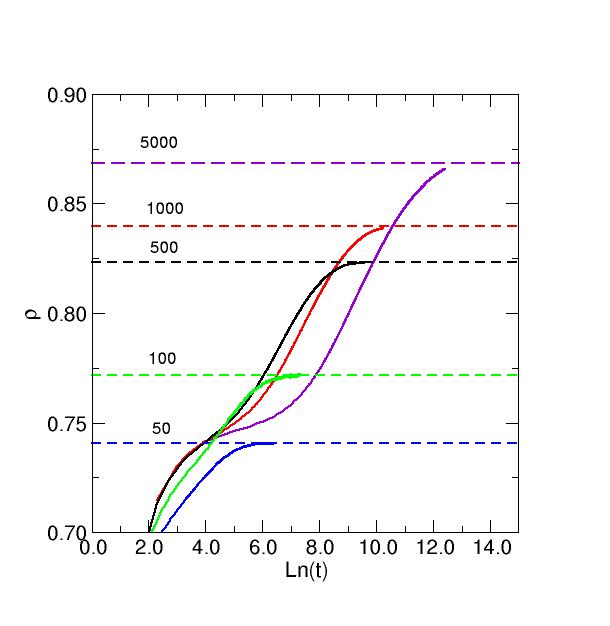
The following graph shows the evolution of the density for different
values of K (shown as different colors) obtained from a numerical
simulation of the model. In all
cases, the density evolves towards a steady state value (indicated by
the dashed lines). The steady state density increases as K increases
(and approaches one in the limit of infinite K). Note that, for large
K, the density increases very
slowly (it's a log scale).
At large values of K, there are three distinct regimes as
shown:
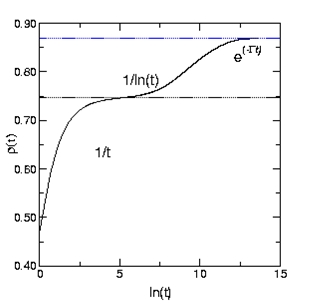
The first regime, where the density varies as 1/t, is characteristic of
irreversible adsorption. At much larger times, rods start to desorb and
large-scale reorganizations take place that create additional space,
allowing the insertion of extra rods. The kinetics is now characterized
by
1/ln(t) and it is this behavior that has been observed in some granular
compaction experiments. Finally at still longer times, there is an
exponential approach to the steady state.
To run a Java simulation of the two-dimensional PLM, written by John
Parry, Click here
For more information, see:
Talbot, J., G. Tarjus, P. R. Van Tassel and P. Viot, “From Car Parking
to Protein
Adsorption: A Review of Sequential Addition Processes”, Colloids and
Surfaces A.
165 287-324, 2000.


