2. Suites du type 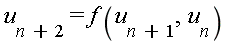
2.1 Suite de Fibonacci : 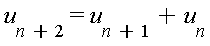
| > |
a:=1:b:=1:for k to 10 do c:=a+b:print(c):a:=b:b:=c:od: |
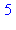
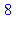
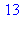
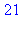
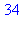
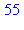
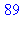
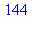
2.2 Fonctions récursives
Il
est possible en Maple, comme en beaucoup d'autres langages (sauf en
Fortran), de définir des fonctions récursives, c'est à dire des
fonctions qui s'appellent elles-mêmes. Ici, par exemple, pour Fibonacci
:
| > |
fib:=n-> if n<=1 then n else fib(n-1)+fib(n-2);fi; |

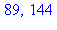
La fonction trace montre le déroulement du calcul :
| > |
trace(fib):fib(4);untrace(fib); |
{--> enter fib, args = 4
{--> enter fib, args = 3
{--> enter fib, args = 2
{--> enter fib, args = 1
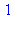
<-- exit fib (now in fib) = 1}
{--> enter fib, args = 0
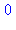
<-- exit fib (now in fib) = 0}
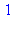
<-- exit fib (now in fib) = 1}
{--> enter fib, args = 1
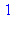
<-- exit fib (now in fib) = 1}
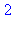
<-- exit fib (now in fib) = 2}
{--> enter fib, args = 2
{--> enter fib, args = 1
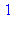
<-- exit fib (now in fib) = 1}
{--> enter fib, args = 0
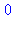
<-- exit fib (now in fib) = 0}
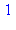
<-- exit fib (now in fib) = 1}
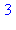
<-- exit fib (now at top level) = 3}
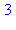
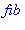
Il
y a eu 9 appels à la fonction fib. De façon générale, on montre qu'il y
a 2 fib(n+1)-1 appels. Si on regarde attentivement le schéma ci-dessus,
on voit qu'il y a plusieurs fois appel à fib(0), fib(1) et
fib(2) ; pour éviter ces répétitions, on utilisera comme ci-dessous,
l'option remember. Il n'y a plus que 5 appels !
| > |
fib:=proc(n) option remember: if n<=1 then n else fib(n-1)+fib(n-2);fi;end; |








2.3 Solution d'équation de récurrence avec rsolve
Le terme général de la suite est obtenu à l'aide de la commande de solution d'équation de récurrence rsolve :
| > |
restart:lapin:={f(n)=f(n-1)+f(n-2),f(1..2)=1}; |
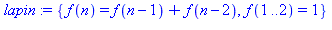
| > |
sol:=rsolve(lapin,f);g:=unapply(factor(sol),n); |
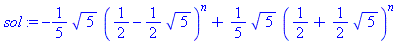
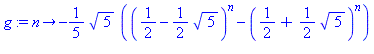
La commande evala donne une évaluation algébrique dans le champ algébrique le plus petit possible :
| > |
evala(g(11)),evala(g(12)); |
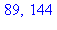
2.4 La commande fibonacci
| > |
combinat[fibonacci](11),combinat[fibonacci](12); |
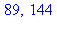
La commande fibonacci de la bibliothèque combinat
marche aussi pour des nombres négatifs et donne de plus les
polynômes de Fibonacci. On peut obtenir le listing de cette fonction
(comme 95% des fonctions de Maple) avec la variable verboseproc mise à 2 :
| > |
interface(verboseproc=2);print(combinat[fibonacci]): |
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_83.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_84.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_85.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_86.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_87.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_88.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_89.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_90.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_91.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_92.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_93.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_94.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_95.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_96.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_97.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_98.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_99.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_100.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_101.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_102.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_103.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_104.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_105.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_106.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_107.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_108.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_109.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_110.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_111.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_112.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_113.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_114.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_115.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_116.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_117.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_118.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_119.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_120.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_121.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_122.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_123.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_124.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_125.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_126.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_127.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_128.gif)
![proc (n, x) local i, b, p, f1, f2, s1, s2, s3, r; option `Copyright (c) 1990 by the University of Waterloo. All rights reserved.`; if type([args], '[integer]') then if n = 0 then return 0 end if; if n...](images/10_06_129.gif)
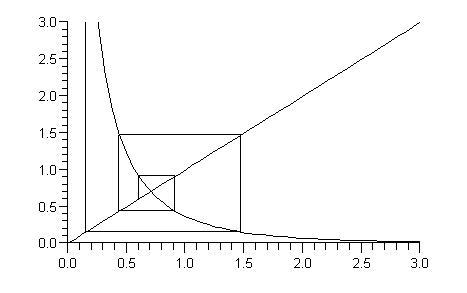
2.5 Série Génératrice
Les valeurs de 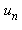 , pour n grand, s'obtiennent à l'aide de la série génératrice définie par
, pour n grand, s'obtiennent à l'aide de la série génératrice définie par ![v := proc (z) options operator, arrow; sum(u[n]*z^n, n = 0 .. infinity) end proc](images/10_06_131.gif) . La commande ztrans de Maple donne la transformée Z de
. La commande ztrans de Maple donne la transformée Z de 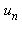 , c'est à dire
, c'est à dire 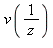 ,
qui est toujours une fraction rationnelle dans le cas de récurrence
linéaire à coefficients constants. Pour les nombres de Fibonacci, les
commandes ci-dessous calculent successivement
,
qui est toujours une fraction rationnelle dans le cas de récurrence
linéaire à coefficients constants. Pour les nombres de Fibonacci, les
commandes ci-dessous calculent successivement 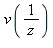 avec les conditions initiales, puis
avec les conditions initiales, puis 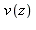 .
.
| > |
restart: rel := ztrans(u(n+2)=u(n+1)+u(n),n,z); |
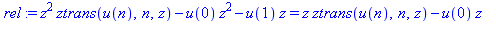

| > |
v := solve( rel, ztrans(u(n),n,z)); |
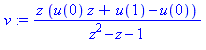
| > |
v := subs({u(0)=0,u(1)=1},v); |
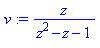
| > |
v := normal(subs(z=1/z,v)); |
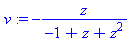
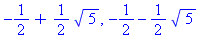
| > |
d:=factor(denom(v),sqrt(5)); |
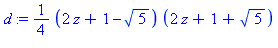
| > |
v:=convert(-z/d,parfrac,z); |
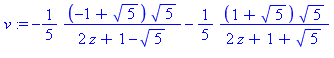
Ci-dessous,
la plus petite racine en valeur absolue sera appelée a (ici a est
l'inverse du nombre d'or) et on calculera le coefficient 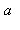 qui lui est relatif. En développant en puissance de z le terme 1/(1-z/a), on obtiendra une approximation de
qui lui est relatif. En développant en puissance de z le terme 1/(1-z/a), on obtiendra une approximation de 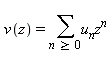 et en particulier
et en particulier 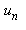 sera approximé par a/
sera approximé par a/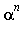
| > |
alpha:=-1/2+1/2*sqrt(5); |
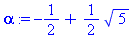
| > |
principal:=op(2,v);
a:=subs(z=0,principal); |
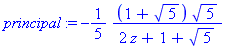
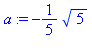
On
doit remarquer que les coefficients en z du développement de Taylor
ci-dessous donnent bien les nombres de Fibonacci, même pour des valeurs
de n petites (n=9, 10, 11) :
| > |
evalf(taylor(principal,z,12)); |
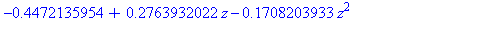
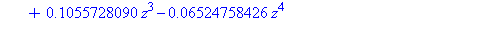
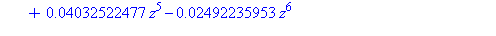
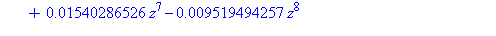
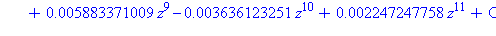

| > |
evalf(a/alpha^9),combinat[fibonacci](9);
evalf(a/alpha^10),combinat[fibonacci](10);
evalf(a/alpha^11),combinat[fibonacci](11); |
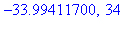
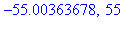

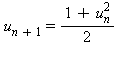 :
: 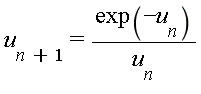
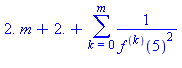
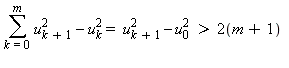 ?
?
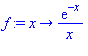
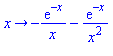
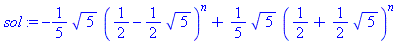
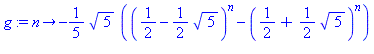
![v := proc (z) options operator, arrow; sum(u[n]*z^n, n = 0 .. infinity) end proc](images/10_06_131.gif) . La commande ztrans de Maple donne la transformée Z de
. La commande ztrans de Maple donne la transformée Z de 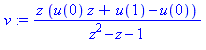
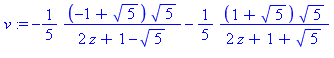
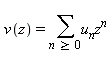 et en particulier
et en particulier 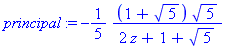
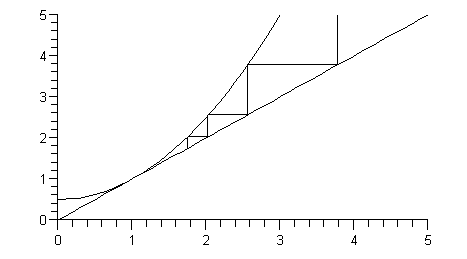
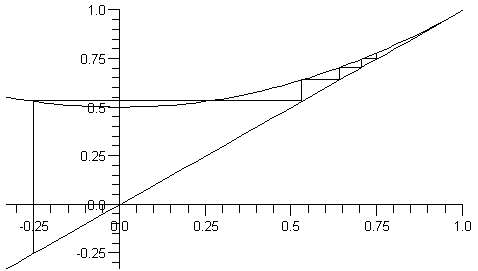
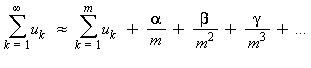 Pour m assez grand les termes correctifs sont de plus en plus petits.
On cherche tout d'abord à déterminer par tatonnements a et ß :
Pour m assez grand les termes correctifs sont de plus en plus petits.
On cherche tout d'abord à déterminer par tatonnements a et ß : 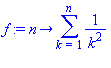
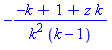
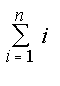 : factor(sum(i,i=1..n));
: factor(sum(i,i=1..n)); 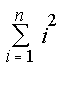 : factor(sum(i^2,i=1..n));
: factor(sum(i^2,i=1..n)); 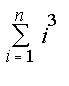 : factor(sum(i^3,i=1..n));
: factor(sum(i^3,i=1..n)); 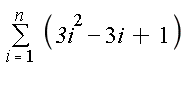 : factor(sum(3*i^2-3*i+1,i=1..n));
: factor(sum(3*i^2-3*i+1,i=1..n)); 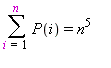 :
: