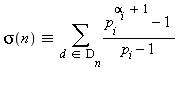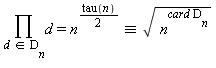Chap. 3 : Fonctions et procédures
1. Création de fonctions
L'opérateur flèche -> (taper successivement - et >) permet de créer des fonctions qui donnent des expressions
| > |
f1:=x->x^2+a; # déclaration de fonction d'une variable |
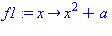
| > |
f1(3); # utilisation de la fonction |
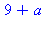
| > |
f2:=(x,y)->x^2+y^2+1; # déclaration de fonction de 2 variables |
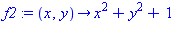
| > |
f2(2,b); # utilisation de la fonction |
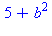
Inversement, à partir d'une expression algébrique, on peut obtenir une fonction à l'aide de l'opérateur unapply.
| > |
f3:=unapply(x^2+y^2+1,y); |
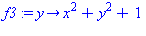
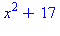
2. Formules sommatoires
L'opérateur subs permet de substituer une suite de termes dans une expression. Par exemple :
| > |
expression := a*k^2 + b*k; |
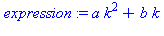
| > |
subs({a=1/2,b=3/2},expression); |
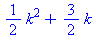
En général, si on veut calculer S = f(1)+f(2)+...+f(n), on cherche une fonction F(k) telle que f(k) = F(k)-F(k-1) ; on a alors S = F(n)-F(0). Le problème est donc de déterminer F. Il est normal d'essayer de mettre F sous la forme d'un polynôme de degré égal au degré de f + 1.
Montrer ainsi que : 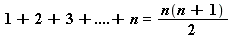
| > |
restart:F:=k->a*k^2+b*k;
Equation:=expand(F(k)-F(k-1)-k);
solution:=solve({coeffs(Equation,k)});
F2:=unapply(subs(solution,F(k)),k);
factor(F2(n)-F2(0)); |
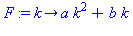
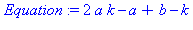
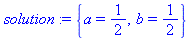
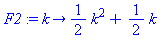
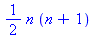
Montrer ainsi que : 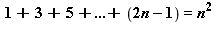
| > |
restart:F:=k->a*k^2+b*k:
Equation:=expand(F(k)-F(k-1)-(2*k-1));
solution:=solve({coeffs(Equation,k)});
F2:=unapply(subs(solution,F(k)),k);
factor(F2(n)-F2(0)); |
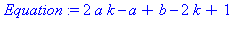
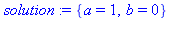
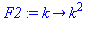
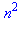
Une autre voie est d'utiliser la fonction sum, mais ce n'est pas le but principal de cet exercice qui est d'introduire une procédure comme on le verra par la suite.
| > |
factor(sum(2*k-1,k=1..n)); |
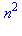
Donc la première méthode va être généralisée à l'aide d'une procédure : ![n[i]](images/10_03_21.gif) et
et ![n[f]](images/10_03_22.gif) désignant les valeurs initiales et finales de la variable
désignant les valeurs initiales et finales de la variable 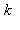 dans l'expression
dans l'expression 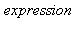 :
:
| > |
SolveGen:=proc(expression,k,ni,nf)
local i,deg,F,eq,sol,Fgen,a, Equation, solution;
deg:=degree(expression,k);
F:=unapply(add(a[i]*k^i,i=1..deg+1),k);
Equation:=expand(F(k)-F(k-1)-expression);
solution:=solve({coeffs(Equation,k)},{seq(a[i],i=1..deg+1)});
Fgen:=unapply(subs(solution,F(k)),k);
eq:=factor(Fgen(nf)-Fgen(ni-1));
print(Sum(expression,k=ni..nf)=eq);
end: |
Cette procédure donne alors les formules sommatoires directement :
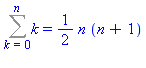
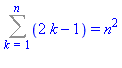
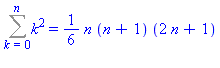
| > |
SolveGen((2*k-1)^2,k,1,n); |
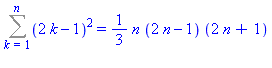
| > |
SolveGen(k*(k+1),k,0,n); |
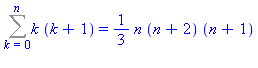
| > |
SolveGen(k*(k+1)*(k+2),k,0,n); |
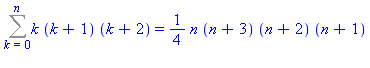
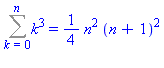
| > |
SolveGen((2*k-1)^3,k,1,n); |
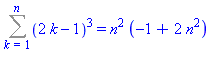
Remarquer que dans la définition de SolveGen, l'opérateur Sum est écrit avec un S majuscule : dans Maple, il arrive souvent que les opérateurs - écrits avec une première lettre majuscule - ne sont pas effectués mais simplement définis. Remarquer que dans l'output le signe 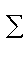 n'est alors pas écrit en bleu mais en noir. Par contre, avec un s minuscule, l'opération s'effectue et on a :
n'est alors pas écrit en bleu mais en noir. Par contre, avec un s minuscule, l'opération s'effectue et on a :
| > |
'sum(2*k-1,k=1..n)'=sum(2*k-1,k=1..n); |
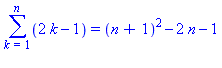
La commande 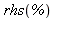 désignant le membre de droite de l'équation précédente, on termine par :
désignant le membre de droite de l'équation précédente, on termine par :
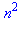
3. Fonctions et opérateur modulo
3.1. Equations modulo
La commande msolve donne les solutions d'une équation, modulo le nombre donné en second argument :
| > |
restart:Equation:= 15*x = '21 mod 28';sol:=msolve(Equation,28); |
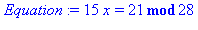
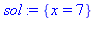
En effet 7*15 = 105 et 105 mod 28 = 21 La fonction rhs (right hand side) donne la partie de droite d'une équation. La commande irem donne le reste entier d'une division par le second argument, ce qui confirme le résultat précédent :
| > |
irem(15*rhs(sol[1]),28), 7*15 mod 28; |
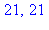
On trouve 6 solutions pour l'équation suivante :
| > |
Equation:= 36*x = '54 mod 42'; sol:=msolve(Equation,42); |
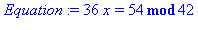
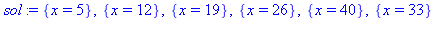
Vérification (noter la facilité donnée par la commande in sol) :
| > |
for k in sol do irem(36*rhs(op(k)),42) od; |
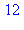
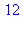
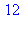
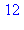
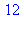
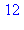
3.2. Congruence et polynômes
On utilisera 3 méthodes pour démontrer que : 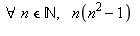
 est divisible par 6 :
est divisible par 6 :
1. Par récurrence : en définissant f := n-> n*(n^2-1), la différence de deux termes consécutifs, d := f(n+1)-f(n)}, est mise en facteurs par factor(d) on trouve 3n(n+1). Divisible par 3, cette expression est également divisible par 2 puisque c'est le produit de deux nombres consécutifs
| > |
restart:f:=n->n*(n^2-1); |
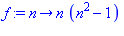
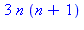
et on vérifie que le démarrage est correct :

2. En raisonnant sur les nombres qui se suivent comme plus haut, Factor forme inerte (pas d'exécution) de factor est employée pour factoriser des
polynômes sur un domaine, ici avec mod.
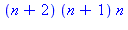
3. La commande msolve(eqns,n)} résout les équations en équations sur les entiers modulo n. Ainsi msolve(f(n), 6)} donne n = n, ce qui signifie que tous les entiers sont solutions de
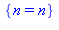
Montrer de même que 
| > |
f:=n->n*(n^4-1);factor(f(n+1)-f(n));f(2); |
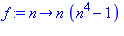
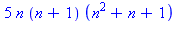
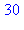
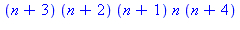
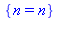
Montrer de même que 
| > |
f:=n->n*(n^6-1);factor(f(n+1)-f(n));f(2); |
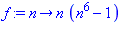
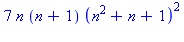
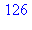
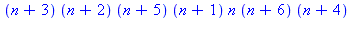
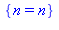
3-3. Congruence et exposants
Montrer que 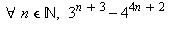 est divisible par 11
est divisible par 11
| > |
f:=n->3^(n+3)-4^(4*n+2); |
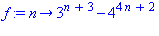
La commande a retourné l'ensemble vide, ce qui signifie qu'il n'y a pas de solution ! Pourtant, n=1, 2, 3, 4 sont solutions de 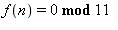 :
:
| > |
for i to 4 do irem(f(i),11);od; |
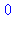
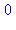
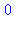
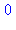
Il faut savoir que Maple "n'aime" pas les exposants trop compliqués, aussi on remplace 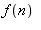 par la fonction identique
par la fonction identique 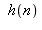 et on trouve que toute valeur de
et on trouve que toute valeur de 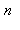 est bonne :
est bonne :
| > |
h:=n->27*3^n-16*256^n;msolve(h(n),11); |
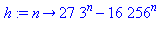
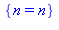
On peut également remarquer que les deux termes de 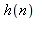 sont égaux modulo 11 :
sont égaux modulo 11 :
| > |
27*3^n mod 11;16*256^n mod 11; |
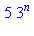
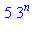
4. Exponentiation rapide
Ci-après, on donne une procédure calculant un nombre 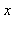 à la puissance
à la puissance 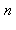 en le multipliant
en le multipliant 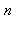 fois par lui-même :
fois par lui-même :
| > |
ma_procedure:=proc(x,n)
local m,resul:
resul:=1:
for m to n do resul:=resul*x:od:
resul;end; |








| > |
ma_procedure(2,3),ma_procedure(3,4); |
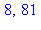
La commande trace permet de suivre le déroulement des opérations (et éventuellement voir les erreurs !) :
| > |
trace(ma_procedure):ma_procedure(2,3);untrace(ma_procedure): |
{--> enter ma_procedure, args = 2, 3
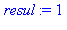
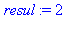
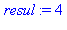
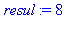
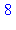
<-- exit ma_procedure (now at top level) = 8}
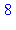
Même effet si on affecte à la variable printlevel une valeur plus grande que la valeur par défaut égale à 1 :
| > |
printlevel:=10:ma_procedure(2,3);printlevel:=1: |
{--> enter ma_procedure, args = 2, 3
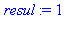
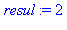
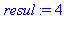
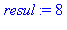
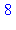
<-- exit ma_procedure (now at top level) = 8}
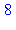
La procédure ci-dessus n'est pas très efficace pour calculer des nombres à une grande puissance. Ci-dessous on calcule le temps mis pour obtenir 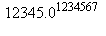 :
:
| > |
depart:=time():ma_procedure(12345.0,1234567);arrivee:=time()-depart; |
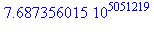
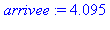
Maple sait calculer beaucoup plus rapidement, ce qui montre qu'il utilise un procédé d'exponentiation rapide :
| > |
depart:=time():12345.0^1234567;arrivee:=time()-depart; |
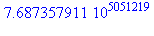
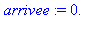
On donne ci-dessous une méthode d'exponentiation rapide en utilisant les développements en puissance de 2 : par exemple 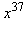 se décompose en
se décompose en 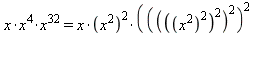 ce qui réduit le nombre de multiplications de 36 à 7
ce qui réduit le nombre de multiplications de 36 à 7
| > |
expo:=proc(xx,nn)
local x,resul,n;
x := xx; n := nn; resul := 1;
while(n>0) do
if type(n,odd) then resul:=resul*x;n:=n-1;
else x:=x*x;n:=n/2;
fi;
od;
resul;
end; |
















On vérifie que cette méthode est beaucoup plus rapide que la précédente :
| > |
depart:=time():expo(12345.0,1234567);arrivee:=time()-depart; |
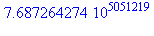
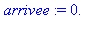
5. Euclide et le pgcd
L'algorithme d'Euclide permet de trouver le pgcd de deux nombres. Il peut être résumé de la façon suivante : on effectue les divisions euclidiennes successives :
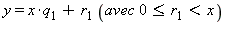
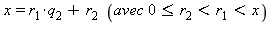
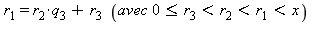 etc
etc
La suite de ces opérations s'arrête nécessairement comme le montrent les inégalités obtenues. On stoppe l'itération au premier reste nul. La procédure est très simple :
| > |
euclide:=proc(x,y)
local r, xx,yy:
r:=irem(y,x):
yy:=y:
xx:=x:
while r>0 do yy:=xx: xx:=r: r:=irem(yy,xx):od:
xx;
end; |












On vérifie et on compare avec la fonction igcd de Maple qui donne directement le pgcd de deux nombres :
| > |
euclide(21,45), igcd(45,21); |
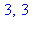
| > |
euclide(210,45), igcd(45,210); |
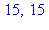
6. Théorème des restes chinois
Si 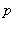 et
et 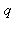 sont premiers entre eux, leur pgcd est égal à 1 par définition et le théorème de Bezout assure l'existence de deux nombres
sont premiers entre eux, leur pgcd est égal à 1 par définition et le théorème de Bezout assure l'existence de deux nombres 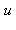 et
et 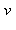 tels que
tels que 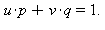 La commande igcd donne le pgcd des deux nombres et la commande étendue igcdex retourne les coefficients
La commande igcd donne le pgcd des deux nombres et la commande étendue igcdex retourne les coefficients 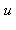 et
et 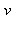 . Ainsi, 27 et 40 étant premiers entre eux :
. Ainsi, 27 et 40 étant premiers entre eux :
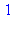
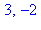
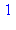
La relation ci-dessus est utilisée pour résoudre les systèmes de congruence du type suivant : 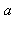 et
et 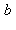 étant deux entiers relatifs donnés, déterminer les entiers
étant deux entiers relatifs donnés, déterminer les entiers 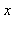 tels que
tels que 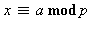 et
et 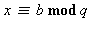 L'entier
L'entier 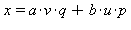 vérifie les deux égalités précédentes car
vérifie les deux égalités précédentes car 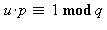 et
et 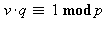 . Résoudre par exemple
. Résoudre par exemple 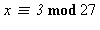 et
et 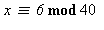 et vérifier.
et vérifier.
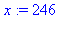
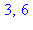
La librairie numtheory, chargée par l'ordre with(numtheory), contient la fonction mcombine qui donne directement la valeur de 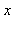 .
.
| > |
with(numtheory):mcombine(27,3,40,6); |
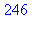
Souvent Maple offre différentes solutions pour un même problème : ainsi, la librairie générale contient la fonction chrem (pour chinese remainder) qui donne directement la valeur de 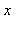 . Ces considérations sont souvent utilisées pour traiter les très grands nombres.
. Ces considérations sont souvent utilisées pour traiter les très grands nombres.
| > |
chrem( [3,6], [27,40] ); |
7. La fonction d'Euler
La fonction d'Euler φ est définie, pour tout 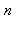 , par le nombre d'entiers positifs premiers avec
, par le nombre d'entiers positifs premiers avec 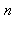 et plus petits que
et plus petits que 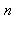 . Cette fonction est donnée par la commande phi après avoir chargé la librairie qui la contient par with(numtheory).
. Cette fonction est donnée par la commande phi après avoir chargé la librairie qui la contient par with(numtheory).
| > |
restart: with(numtheory): n:=200: phi(n); |
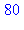
1. Vérifier le résultat précédent :
| > |
resul:=0:
for i to n do
if igcd(i,n)=1 then resul:=resul+1: fi;
od:
resul; |
2. La liste des diviseurs de 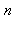 , notée par la suite
, notée par la suite 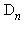 , étant obtenue par la commande divisors, vérifier la relation
, étant obtenue par la commande divisors, vérifier la relation 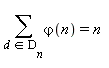 :
:
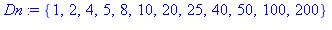
| > |
resul:=0:
for d in Dn do
resul:=resul+phi(d):
od:
resul; |
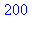
3. Vérifier que les 80 nombres 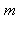 premiers avec 200 et inférieurs à 200 obéissent à la relation
premiers avec 200 et inférieurs à 200 obéissent à la relation 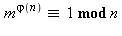 . (faute de place, on s'arrête ici à m=10)
. (faute de place, on s'arrête ici à m=10)
| > |
for m to 10 do if igcd(m,200)=1 then print(m^phi(200) mod 200) fi:od: |
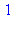
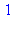
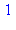
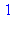
4. La commande ifactor donnant la décomposition de 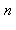 en facteurs premiers et
en facteurs premiers et ![p[i]](images/10_03_191.gif) étant ces facteurs premiers, vérifier que
étant ces facteurs premiers, vérifier que ![phi(n) = n*(product(1-1/p[i], i)); -1](images/10_03_192.gif)
| > |
prod:=ifactor(n); expand(prod); |
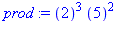
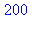
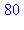
5. Vérifier sur quelques exemples que, si 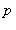 et
et 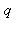 sont premiers entre eux,
sont premiers entre eux, 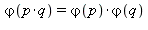
| > |
for p to 3 do
for q to 3 do
if igcd(p,q)=1 then print(p,q,phi(p)*phi(q),phi(p*q)) fi:
od:
od: |
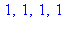
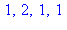
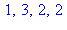
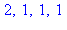
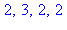
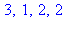
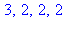
8. Décomposition en facteurs premiers
Un entier 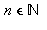 se décompose en produit de facteurs premiers
se décompose en produit de facteurs premiers ![p[i]](images/10_03_207.gif) , la commande ifactor donnant cette décomposition. D'autre part, après avoir chargé la librairie relative à la théorie des nombres par with(numtheory), la commande factorset donne l'ensemble des
, la commande ifactor donnant cette décomposition. D'autre part, après avoir chargé la librairie relative à la théorie des nombres par with(numtheory), la commande factorset donne l'ensemble des ![p[i]](images/10_03_208.gif) . Essayer ces deux commandes en prenant
. Essayer ces deux commandes en prenant 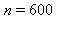 .
.
| > |
restart: with(numtheory):
n := 600:
prod := ifactor(n); expand(prod);
factorset(n); |
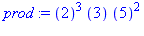
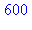
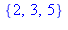
1. La liste des diviseurs de 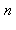 , notée par la suite
, notée par la suite 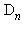 , s'obtient par la commande divisors. Le cardinal de
, s'obtient par la commande divisors. Le cardinal de 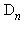 est donné par la commande tau et la somme des diviseurs s'obtient par la commande sigma. Vérifier les résultats donnés par tau et sigma.
est donné par la commande tau et la somme des diviseurs s'obtient par la commande sigma. Vérifier les résultats donnés par tau et sigma.
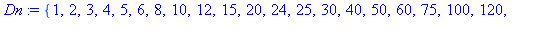

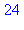
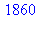
| > |
restau := 0: ressig := 0:
for elem in Dn do
restau:=restau+1:
ressig:=ressig+elem:
od:
restau,ressig; |
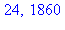
2. On se propose de vérifier numériquement la relation 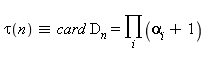 où les
où les![alpha[i]](images/10_03_222.gif) désignent les exposants des facteurs premiers apparaissant dans la décomposition de
désignent les exposants des facteurs premiers apparaissant dans la décomposition de 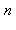 .
.
| > |
res:=1:
for d in prod do
if nops(d)=1 then alpha:=1
else alpha:=op(2,d): fi;
res:=res*(1+alpha):
od:
res; |
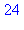
3. On démontrera de même que la valeur retournée par sigma vérifie 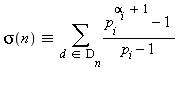
| > |
res:=1:
for d in prod do
p:=op([1,1],d):
if nops(d)=1 then alpha:=1 else alpha:=op(2,d): fi;
res:=res*(p^(1+alpha)-1)/(p-1):
od:
res; |
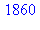
4. De la même façon, on vérifiera que 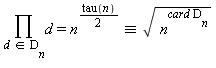
| > |
res:=1:
for d in Dn do
res:=res*d;
od:
res; |
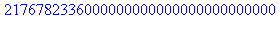
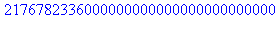
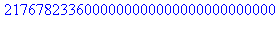
![]()
![]()
![]()
![]()
![]()
![]()
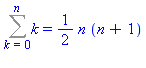
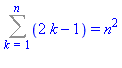
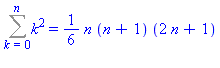
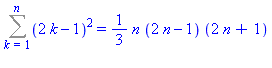
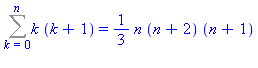
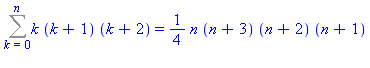
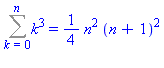
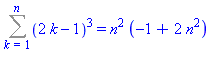
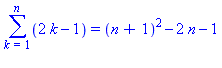
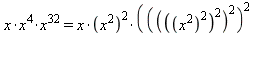 ce qui réduit le nombre de multiplications de 36 à 7
ce qui réduit le nombre de multiplications de 36 à 7 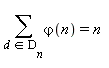 :
: ![phi(n) = n*(product(1-1/p[i], i)); -1](images/10_03_192.gif)
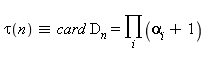 où les
où les