2. Suites, ensembles et listes
Il ne faut pas confondre les suites, les ensembles et les listes
2.1 Suites
Les suites sont créées en séparant les objets par une virgule. Il faut respecter l'ordre : ainsi 1,2,3 est différent de 2,1,3.
| > |
restart: suite := 1,2,3,2,3; |
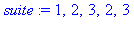
La fonction seq permet de créer facilement des suites :
| > |
seq(cos(i*Pi/6),i=1..3); |
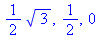
2.2 Ensembles
Un ensemble est créé par une suite non ordonnée d'expressions distinctes et entourée par deux accolades, { et }. Ainsi l'ensemble {1,2,3}est égal à {2,3,1,1,3}.
L'opérateur evalb évalue si une expression est vraie ; avec la suite précédente, on vérifie l'égalité :
| > |
evalb( {suite} = {3,2,1} ); |

2.3 Listes
Une liste est créée par une suite ordonnée d'expressions qui peuvent être identiques et entourée par deux crochets, [ et ]. Les listes peuvent être imbriquées les unes dans les autres.
| > |
liste_1 := [1,2,3];
liste_2 := [3,4,5];
liste_3 := [liste_1,liste_2]; |
![[1, 2, 3]](images/10_02_14.gif)
![[3, 4, 5]](images/10_02_15.gif)
![[[1, 2, 3], [3, 4, 5]]](images/10_02_16.gif)
Les éléments d'une liste (contenus entre les deux crochets) sont obtenus par l'opérateur op :
| > |
liste_4 := [op(liste_1),op(liste_2)]; |
![[1, 2, 3, 3, 4, 5]](images/10_02_17.gif)
le i-ème élément d'une liste est donnépar op(i,list).
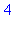
La liste_2 étant la liste précédente, on peut également obtenir un de ses éléments en donnant son rang entre crochets et on peut modifier la valeur de cet élément :
| > |
liste_2[3];
liste_2[3] := 67;
liste_2;
|
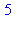
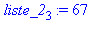
![[3, 4, 67]](images/10_02_21.gif)
Par contre on ne peut pas supprimer un élément d'une liste, par exemple en lui affectant la valeur NULL qui est l'élément neutre des suites d'expressions. Pour supprimer un élément d'une liste, il faut utiliser la commande subsop
Error, expression sequences cannot be assigned to lists
| > |
liste_n := subsop(2=NULL,liste_2);
liste_n; |
![[3, 67]](images/10_02_22.gif)
![[3, 67]](images/10_02_23.gif)
4. Fractions continues
Le développement en fraction continue d'un nombre r est donné par la relation :
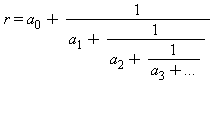
où ![a[0]](images/10_02_39.gif) est la partie entière de r (en Maple trunc(r)) et le reste est sa partie fractionnaire (en Maple frac(r)). Les éléments réduits (mis sous la forme numérateur/dénominateur) de la suite
est la partie entière de r (en Maple trunc(r)) et le reste est sa partie fractionnaire (en Maple frac(r)). Les éléments réduits (mis sous la forme numérateur/dénominateur) de la suite
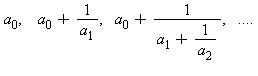
fournissent des approximations rationnelles successives (convergents} de r. On montre assez facilement que si r est un rationnel, cette suite est finie ; par contre, elle est infinie si r est irrationnel. En Maple, après avoir chargé la bibliothèque numtheory par la commande with(numtheory), le développement en fraction continue est obtenu par cfrac(r,n) où n désigne éventuellement l'ordre du dernier convergent ; par exemple, le développement en fraction continue de 17/23 (par défaut jusqu'au dixième ordre, en fait, c'est un rationnel et n=5) est donné par :
| > |
restart: with(numtheory): '17/23' = cfrac(17/23); |
![17/23 = CFRAC([0, 1, 2, 1, 5])](images/10_02_41.gif)
La liste des entiers dans les dénominateurs est obtenue par la commande convert(r,confrac) et la liste des convergents peut être mise dans un troisième argument (optionnel)
| > |
`liste des a_i` = convert(17/23,confrac,convergents);
'convergents' = convergents; |
![`liste des a_i` = ([0, 1, 2, 1, 5])](images/10_02_42.gif)
![convergents = ([0, 1, 2/3, 3/4, 17/23])](images/10_02_43.gif)
Si on change 17/23 par 25/23, on obtient un message d'erreur :
| > |
`liste des a_i` = convert(25/23,confrac,convergents); |
Error, (in convert/confrac/numeric) invalid arguments
Le premier appel à convert a donné une valeur à la variable convergents et le second appel à la même commande ne peut plus changer cette valeur. Il faut libérer la variable de cette valeur (vider la mémoire, ou plutôt la rendre disponible en l'entourant de deux cotes).
D'où cette remarque très générale : entourer une variable entre des accents aigus (') permet d'appeler le nom de la variable et non sa valeur. Pour libérer la valeur d'une variable, on affecte son nom à la valeur de la variable par :
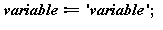
Bien suivre les opérations suivantes :
| > |
n := 15; # On met le nombre 15 dans la mémoire d'adresse n
n; # On vérifie le contenu de la mémoire
n := 'n'; # Le contenu de la mémoire est écrasée
n; # La mémoire d'adresse n est vide |
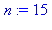
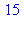
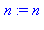
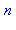
| > |
`liste des a_i` = convert(25/23,confrac,'convergents'); 'convergents' = convergents; |
![`liste des a_i` = ([1, 11, 2])](images/10_02_49.gif)
![convergents = ([1, 12/11, 25/23])](images/10_02_50.gif)
Les commandes données ci-dessous seront exécutées pour analyser trois types de nombres.
1 - L'expression evalf(17/23,20) donne une approximation à vingt chiffres significatifs du nombre rationnel 17/23 ; donc c'est aussi un nombre rationnel : son développement en fraction continue sera comparé avec celui de 17/23 ci-dessus.
| > |
`approximation de 17/23` = evalf(17/23,20); |
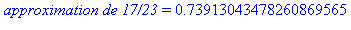
| > |
'evalf(17/23)' = cfrac(evalf(17/23,20)); |
![evalf(17/23) = CFRAC([0, 1, 2, 1, 4, 1, 869565217391304347])](images/10_02_52.gif)
| > |
`liste des a_i` = convert(evalf(17/23,20),confrac,'convergents');
'convergents' = convergents; |
![`liste des a_i` = ([0, 1, 2, 1, 4, 1])](images/10_02_53.gif)
![convergents = ([0, 1, 2/3, 3/4, 14/19, 17/23])](images/10_02_54.gif)
2 - Pi est un nombre irrationnel : la suite de ses convergents est une suite infinie non périodique.
![Pi = CFRAC([3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, `...`])](images/10_02_55.gif)
| > |
`liste des a_i` = convert(Pi,confrac,'convergents');
'convergents' = convergents; |
![`liste des a_i` = ([3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3])](images/10_02_56.gif)
![convergents = ([3, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, 208341/66317, 312689/99532, 833719/265381, 1146408/364913, 4272943/1360120])](images/10_02_57.gif)
![convergents = ([3, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, 208341/66317, 312689/99532, 833719/265381, 1146408/364913, 4272943/1360120])](images/10_02_58.gif)
3 - La racine carrée d'un polynôme du deuxième degré est un nombre irrationnel : on vérifie que la suite de ses convergents est infinie et périodique. La commande solve donne les solutions par rapport à la variable -donnée en deuxième argument- de l'expression donnée en premier argument qui, sauf précision contraire, est supposée par défaut être égale à zéro.
| > |
solutions := solve(x^2+7*x+2,x); |
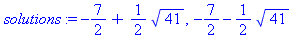
On prend la première racine :
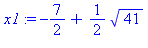
![x1 = CFRAC([-1, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, `...`])](images/10_02_61.gif)
Remarquer que ci-dessous, on obtient la partie entière plus 10 éléments de la partie fractionnaire:
| > |
`liste des a_i` = convert(x1,confrac,'convergents');
'convergents' = convergents; |
![`liste des a_i` = ([-1, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5])](images/10_02_62.gif)
![convergents = ([-1, 0, -1/3, -2/7, -3/10, -17/57, -20/67, -57/191, -134/449, -191/640, -1089/3649])](images/10_02_63.gif)
![convergents = ([-1, 0, -1/3, -2/7, -3/10, -17/57, -20/67, -57/191, -134/449, -191/640, -1089/3649])](images/10_02_64.gif)
Par contre cidessous on a la partie entière plus 30 éléments et une périodicité plus évidente :
| > |
cfrac(x1,30,'quotients'); |
![[-1, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, `...`]](images/10_02_65.gif)
![[-1, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, `...`]](images/10_02_66.gif)
5. Bases et codage
5.1. Opérateur convert
Les nombres sont écrits ou pensés dans différentes bases, c'est-à-dire par paquets, puis paquets de paquets, etc. Certes, la base décimale est maintenant la plus utilisée, mais on groupe toujours les minutes par 60 pour faire des heures, les oeufs par boîtes de 12, le quart de beurre correspond à un huitième de kilo, etc. Cette manière de grouper est devenue tout à fait inconsciente sauf quand pour régler 34 euros vous donnez trois billets de 10 euros et quatre pièces de 1 euro. Maple permet cette analyse par la commande convert(x,base,n) qui retourne une liste du type [ unité, dizaine, centaine, ... ], c'est-à-dire que x est écrit dans un système de base n sous la forme
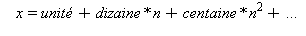
| > |
restart: liste := convert(753,base,10); |
![[3, 5, 7]](images/10_02_68.gif)
le nombre de termes de cette liste est obtenu par la commande nops :
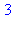
5.2 Instruction d'itération for
L'instruction for permet d'exécuter de manière répétée une instruction (ou un bloc d'instructions), toujours entre do et od (mots réservés), en modifiant la valeur d'une variable de contrôle puis en la comparant à une valeur limite avant chaque début de boucle. Par exemple, l'instruction suivante permet d'imprimer les nombres de 7 en 7, à partir de 4 et jusqu'à 30
| > |
for i from 4 by 7 to 30 do
print(i)
od; |
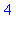
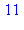
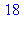
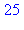
Reconstruire un nombre en base 10 à partir de la liste fournie par convert :
| > |
liste:=convert(753,base,10); |
![[3, 5, 7]](images/10_02_74.gif)
Il faut d'abord initialiser les variables :
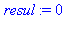
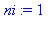
Remarquer la simplicité du déroulement avec la commande for element in liste ; ici on n'a pas besoin d'une variable supplémentaire de contrôle :
| > |
for element in liste do
resul := resul + element*ni;
ni := ni*10:
print('resul' = resul)
od: |
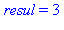
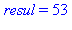
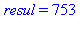
5.3 Boucles imbriquées
Imbriquer des boucles itératives for ou conditionnelles while est une pratique très courante en programmation. Par exemple, en utilisant les paragraphes précédents, on écrit le programme suivant qui compte le nombre de nombres écrits en base dix, compris entre 1 et 715 et où ne figure pas le chiffre 3 ; on doit trouver 499 :
| > |
total := 0:
for nombre to 715 do
liste:=convert(nombre,base,10):
a_garder:=true:
for ii to nops(liste) do
if liste[ii]=3 then
a_garder:=false:
fi;
od:
if a_garder then
total := total+1:
fi:
od:
total; |
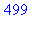
5.4 Codage binaire
La décomposition des nombres en base 2 (base binaire) est particulièrement importante en informatique : on ou off ! Bien observer la décomposition binaire des 8 premiers nombres :
| > |
restart:
for i to 8 do
i = convert(i,base,2);
od; |
![1 = [1]](images/10_02_81.gif)
![2 = ([0, 1])](images/10_02_82.gif)
![3 = ([1, 1])](images/10_02_83.gif)
![4 = ([0, 0, 1])](images/10_02_84.gif)
![5 = ([1, 0, 1])](images/10_02_85.gif)
![6 = ([0, 1, 1])](images/10_02_86.gif)
![7 = ([1, 1, 1])](images/10_02_87.gif)
![8 = ([0, 0, 0, 1])](images/10_02_88.gif)
Montrer que [0,1,0,0,0,1] représente le nombre décimal 34.
| > |
liste := [0,1,0,0,0,1]:
resul :=0:
ni := 1:
for element in liste do
resul := resul+element*ni;
ni := ni*2:
print(resul)
od: |
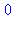
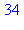
Exercices simples
2.1 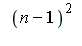 et
et 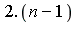 s'écrivent respectivement ab et ba
s'écrivent respectivement ab et ba
En base n, les nombres N= (n-1)^2 et P=2.(n-1) s'écrivent respectivement ab et ba. Le vérifier tout d'abord pour n=9 et n=60. Ce résultat est général. Si on écrit 2*(n-1) sous la forme n-2 + n, le chiffre des unités en base n apparaît être nécessairement égal à n-2 et celui des dizaines est égal à 1.
Faire calculer alors dizaine + unité*n, c'est-à-dire 1 + (n-2)*n, on trouve bien évidemment (n-1)^2.
| > |
restart: N := (n-1)^2; P := 2*(n-1); |
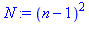
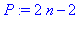
| > |
n := 9: convert(N,base,n); convert(P,base,n); |
![[1, 7]](images/10_02_99.gif)
![[7, 1]](images/10_02_100.gif)
| > |
n := 60: convert(N,base,n); convert(P,base,n); |
![[1, 58]](images/10_02_101.gif)
![[58, 1]](images/10_02_102.gif)
| > |
n := 'n': s := 1+(n-2)*n; factor(s); |
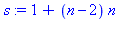
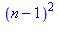
2.2 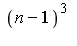 et
et 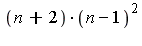 s'écrivent avec les mêmes chiffres
s'écrivent avec les mêmes chiffres
Dans un système de base n (n>3), les nombres Q=(n-1)^3 et R=(n+2).(n-1)^2 s'écrivent avec les mêmes chiffres. Le vérifier pour différentes valeurs de n puis faire un raisonnement général comme ci-dessus avec en plus des centaines.
| > |
restart: Q := (n-1)^3; R := (n+2)*(n-1)^2; |
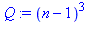
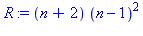
| > |
n := 9: convert(Q,base,n); convert(R,base,n); |
![[8, 2, 6]](images/10_02_109.gif)
![[2, 6, 8]](images/10_02_110.gif)
| > |
n := 60: convert(Q,base,n); convert(R,base,n); |
![[59, 2, 57]](images/10_02_111.gif)
![[2, 57, 59]](images/10_02_112.gif)
| > |
n := 'n': s := n-1+2*n+(n-3)*n^2: factor(s); |
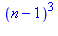
2.3 Couple de nombres premiers jumeaux
Ecrire une boucle sur n variant de 1 à 10 dans laquelle on déterminera si les nombres premiers (donnés par ithprime(i)), successifs et plus petits que n, divisent exactement n ; mettre ces nombres premiers dans une liste. Utiliser ce type de commandes pour déterminer le plus petit couple de nombres premiers jumeaux (c'est à dire de la forme (p, p+2) supérieurs à 30 000.
| > |
restart:
for n from 1 to 10 do
i := 1:
liste := NULL:
while ithprime(i)<n do
if irem(n,ithprime(i))=0 then liste := ithprime(i), liste: fi:
i := i+1:
od:
print('n' = n,' liste' = liste):
od: |
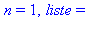
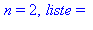
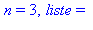
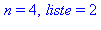
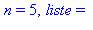
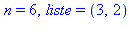
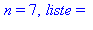
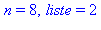
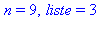
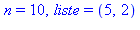
On cherche le premier nombre premier supérieur à 30000 :
| > |
i := 1:
while ithprime(i)<30000 do i := i+1: od:
idep:=i; |
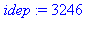
Recherche des nombres premiers jumeaux supérieurs à 30 000 :
| > |
i := idep:
while (ithprime(i)-ithprime(i-1)>2) do
i := i+1:
od:
p := ithprime(i);
q := ithprime(i-1); |
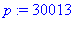
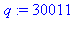
![]()
![]()
![]()
![]()
![]()
![]()
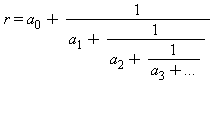
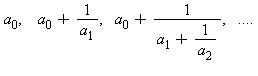
![17/23 = CFRAC([0, 1, 2, 1, 5])](images/10_02_41.gif)
![evalf(17/23) = CFRAC([0, 1, 2, 1, 4, 1, 869565217391304347])](images/10_02_52.gif)
![Pi = CFRAC([3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, `...`])](images/10_02_55.gif)
![x1 = CFRAC([-1, 1, 2, 2, 1, 5, 1, 2, 2, 1, 5, `...`])](images/10_02_61.gif)