 La théorie des bandes permet de classer les cristaux en isolants ou conducteurs électriques en fonction de leur spectre en énergie – organisé en bandes d'énergie permise séparées par des bandes interdites – et de son remplissage en électrons. Si le niveau de Fermi, qui caractérise ce remplissage, est dans une bande permise, c'est un métal ; s'il tombe dans un gap (une bande interdite), c'est un isolant. Un des enseignements principaux de la découverte récente du graphène (2004) et des isolants topologiques est que le spectre des bandes d'énergie n'est pas suffisant pour décrire complètement les propriétés électroniques d'un cristal. En effet la structure de bande complète se compose du spectre en énergie et des fonctions d'onde. Une information essentielle (typiquement, une phase géométrique) est contenue dans les fonctions d'ondes, qui ne transparaît pas dans le spectre. Cette information supplémentaire permet de raffiner la théorie des bandes en distinguant les isolants triviaux (phase géométrique nulle) des isolants topologiques (phase géométrique non-nulle).
La théorie des bandes permet de classer les cristaux en isolants ou conducteurs électriques en fonction de leur spectre en énergie – organisé en bandes d'énergie permise séparées par des bandes interdites – et de son remplissage en électrons. Si le niveau de Fermi, qui caractérise ce remplissage, est dans une bande permise, c'est un métal ; s'il tombe dans un gap (une bande interdite), c'est un isolant. Un des enseignements principaux de la découverte récente du graphène (2004) et des isolants topologiques est que le spectre des bandes d'énergie n'est pas suffisant pour décrire complètement les propriétés électroniques d'un cristal. En effet la structure de bande complète se compose du spectre en énergie et des fonctions d'onde. Une information essentielle (typiquement, une phase géométrique) est contenue dans les fonctions d'ondes, qui ne transparaît pas dans le spectre. Cette information supplémentaire permet de raffiner la théorie des bandes en distinguant les isolants triviaux (phase géométrique nulle) des isolants topologiques (phase géométrique non-nulle).
En collaboration avec des théoriciens de l'institut d'Optique de Palaiseau et du LPS Orsay, nous avons récemment proposé de mesurer cette phase géométrique avec des atomes froids dans un réseau optique réalisant un « cristal artificiel » de type graphène [1]. L'idée est d'utiliser un interféromètre de Stückelberg, qui est l'analogue atomique du célèbre interféromètre optique de Mach-Zehnder. Il se compose de deux séparateurs de faisceau (beam splitter) et de deux chemins: le premier séparateur de faisceau scinde l'onde de matière (i.e. l'atome) en deux, qui évolue ensuite suivant les deux chemins avant d'être recombinée au deuxième séparateur de faisceau. Dans le cas présent, les deux chemins sont deux bandes d'énergie et les séparateurs de faisceau sont des croisements évités entre bandes là où le gap est minimal: un atome peut sauter à travers un gap par effet tunnel. Lors de son trajet sur les deux bandes, l’atome acquiert une différence de phase, ce qui induit un phénomène d’interférence, en principe observable expérimentalement.
Cette proposition est illustrée sur le cas simple d'une structure de bande unidimensionnelle qui dépend de manière continue d'un paramètre de contrôle β permettant de passer d'une phase isolante triviale (0≤β<π/4) à une phase isolante topologique (π/2≥β>π/4) via une phase métallique (β=π/4) à la transition (voir figure ci-dessous).

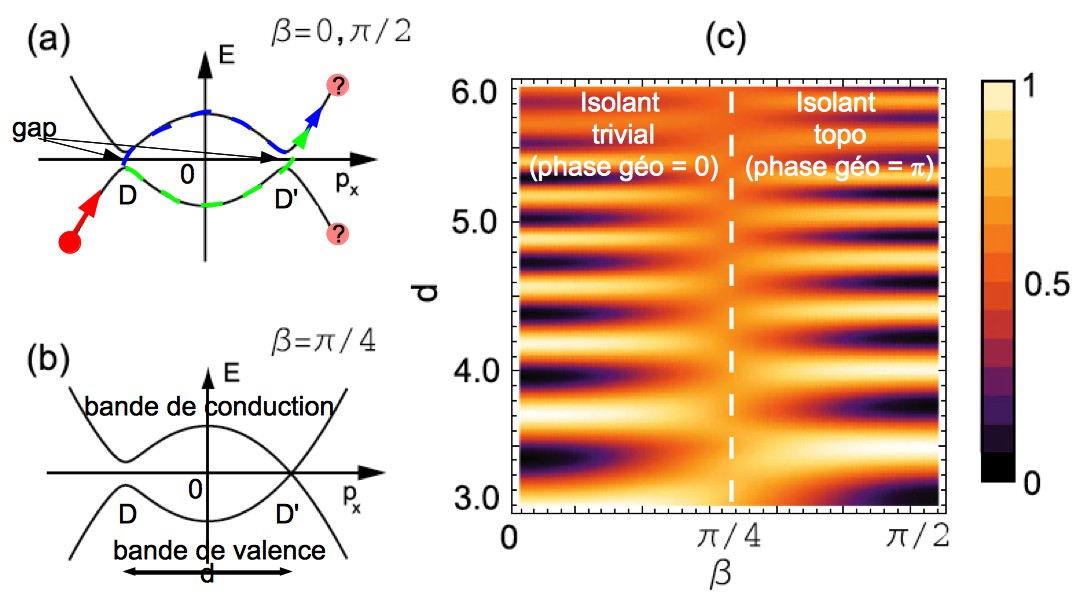
Figure : (a) Relation de dispersion (énergie E en fonction de l'impulsion px) présentant deux croisements évités (D et D') quand β=0 ou π/2. Un atome (en rouge) passe dans l'interféromètre de Stückelberg. (b) Relation de dispersion quand β=π/4. Le gap s'est fermé en D'. (c) Probabilité pour l'atome de terminer dans la bande de conduction en fonction de la distance d entre les deux croisements évités et du paramètre β. Les franges brillantes sont en opposition de phase de part et d'autres de la valeur β=π/4, révélant la présence d'une phase géométrique de π.
Référence: [1] Mass and chirality inversion of a Dirac cone pair in Stückelberg interferometry,
L.K. Lim, J.N. Fuchs et G. Montambaux, Phys. Rev. Lett. 112, 155302 (2014).




